DSA 時間複雜度
執行時間
要完全理解演算法,我們必須瞭解如何評估演算法完成工作所需的時間,即執行時間。
探索演算法的執行時間很重要,因為使用低效的演算法可能會使我們的程式變慢甚至無法使用。
通過了解演算法的執行時間,我們可以選擇適合我們需求的演算法,並且可以使我們的程式執行得更快,並有效地處理更多資料。
實際執行時間
在考慮不同演算法的執行時,我們**不會**關注已實現演算法實際使用的執行時間,原因如下。
如果我們在程式語言中實現一個演算法,並執行該程式,那麼它實際使用的執行時間將取決於許多因素
- 用於實現演算法的程式語言
- 程式設計師如何編寫演算法程式
- 用於執行已實現演算法的編譯器或直譯器
- 執行演算法的計算機硬體
- 計算機上正在執行的作業系統和其他任務
- 演算法正在處理的資料量
由於所有這些不同因素都影響著演算法的實際執行時間,我們怎麼知道一種演算法是否比另一種演算法更快?我們需要找到一種更好的執行時間衡量標準。
時間複雜度
為了評估和比較不同的演算法,與其關注演算法的實際執行時間,不如使用一種稱為時間複雜度的概念更有意義。
時間複雜度比實際執行時間更抽象,並且不考慮程式語言或硬體等因素。
時間複雜度是指演算法在處理大量資料時所需的運算次數。運算次數可以被視為時間,因為計算機對每次運算都使用一定的時間。
例如,在查詢陣列中最小值的演算法中,陣列中的每個值都必須比較一次。每次這樣的比較都可以視為一次運算,而每次運算都需要一定的時間。因此,演算法查詢最小值所需的總時間取決於陣列中的值的數量。
查詢最小值所需的時間因此與值的數量成線性關係。100 個值需要 100 次比較,而 5000 個值需要 5000 次比較。
時間和陣列中值的數量之間的關係是線性的,並可以在如下圖形中顯示
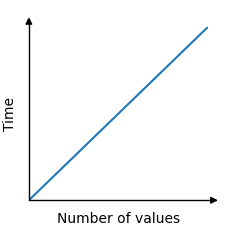
"一次運算"
當這裡談論“運算”時,“一次運算”可能需要一個或幾個 CPU 週期,它只是一個幫助我們進行抽象的詞,這樣我們才能理解什麼是時間複雜度,並找到不同演算法的時間複雜度。
演算法中的一次運算可以理解為我們在演算法的每次迭代中或針對每個資料項執行的操作,這些操作需要恆定的時間。
例如:比較兩個陣列元素,如果一個比另一個大就交換它們,就像氣泡排序演算法所做的那樣,可以被視為一次運算。將此理解為一次、兩次或三次運算,實際上並不會影響氣泡排序的時間複雜度,因為它的時間是恆定的。
我們說一個運算需要“恆定時間”,如果它花費的時間與演算法處理的資料量(\(n\))無關。比較兩個特定的陣列元素,如果一個比另一個大就交換它們,無論陣列包含 10 個還是 1000 個元素,所需的時間都相同。
大 O 符號
在數學中,大 O 符號用於描述函式的上界。
在計算機科學中,大 O 符號更具體地用於查詢演算法的最壞情況時間複雜度。
大 O 符號使用大寫字母 O 加上括號 \(O() \),括號內有一個表示式,表示演算法的執行時間。執行時間通常用 \(n \) 來表示,它是在演算法處理的資料集中的值的數量。
以下是一些演算法大 O 符號的示例,僅供參考
| 時間複雜度 | 演算法 |
|---|---|
| \[ O(1) \] | 查詢陣列中的特定元素,例如 |
| \[ O(n) \] | 查詢最小值。演算法必須對 \(n \) 個值的陣列執行 \(n \) 次運算才能找到最小值,因為演算法必須將每個值比較一次。 |
| \[ O(n^2) \] |
氣泡排序、選擇排序和插入排序是具有此時間複雜度的演算法。它們的時間複雜度原因將在這些演算法的頁面中進行解釋。 大型資料集會顯著減慢這些演算法的速度。僅將 \(n \) 從 100 增加到 200 個值,運算次數就可能增加多達 30000! |
| \[ O(n \log n) \] | 快速排序演算法平均而言比上面提到的三種排序演算法快,其中 \(O(n \log n) \) 是平均情況而不是最壞情況時間。快速排序的最壞情況時間也是 \(O(n^2) \),但正是平均時間使得快速排序如此有趣。我們將在稍後學習快速排序。 |
不同演算法的時間隨值 \(n\) 增加的變化情況如下
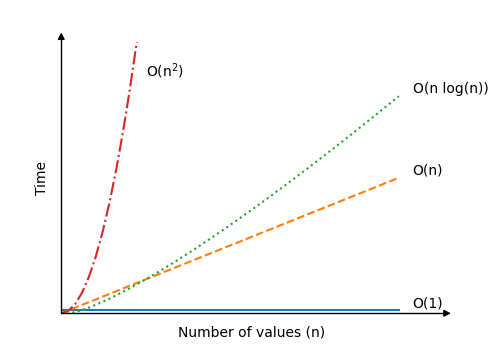
最佳、平均和最壞情況
在解釋大 O 符號時已經提到了“最壞情況”時間複雜度,但演算法如何會有最壞情況場景呢?
查詢具有 \(n \) 個值的陣列中最小值的演算法需要 \(n \) 次運算才能完成,這始終是相同的。所以這個演算法的最佳、平均和最壞情況場景都是相同的。
但是對於我們接下來將要研究的許多其他演算法,如果我們保持值的數量 \(n \) 固定,執行時間仍然會根據實際值發生很大變化。
在不深入所有細節的情況下,我們可以理解排序演算法可以有不同的執行時間,這取決於它正在排序的值。
想象一下,您必須手動將 20 個值從低到高排序
8, 16, 19, 15, 2, 17, 4, 11, 6, 1, 7, 13, 5, 3, 9, 12, 14, 20, 18, 10
這會花費您幾秒鐘完成。
現在,想象您必須對 20 個已經近乎排序的值進行排序
1, 2, 3, 4, 5, 20, 6, 7, 8, 9, 10, 11, 12, 13, 14, 15, 16, 17, 18, 19
您可以非常快地對這些值進行排序,只需將 20 移到列表末尾即可完成,對吧?
演算法的工作方式類似:對於相同數量的資料,它們有時會慢,有時會快。因此,為了能夠比較不同演算法的時間複雜度,我們通常使用大 O 符號來關注最壞情況。
大 O 數學解釋
根據您的數學背景,本節可能難以理解。它旨在為那些需要更全面解釋大 O 的人提供更紮實的數學基礎。
如果您現在不理解,請不要擔心,以後可以回來。如果這裡的數學內容對您來說太難了,也不用太擔心,您仍然可以享受本教程中的各種演算法,學習如何程式設計它們,並理解它們的速度快慢。
在數學中,大 O 符號用於建立函式的上界,而在計算機科學中,大 O 符號用於描述當資料值 \(n\) 增加時演算法執行時間的增長方式。
例如,考慮函式
\[f(n) = 0.5n^3 -0.75n^2+1 \]
函式 \(f\) 的圖如下所示
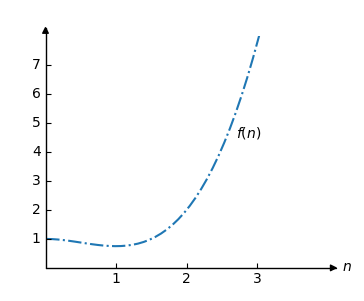
考慮另一個函式
\[g(n) = n^3 \]
我們可以將其繪製如下
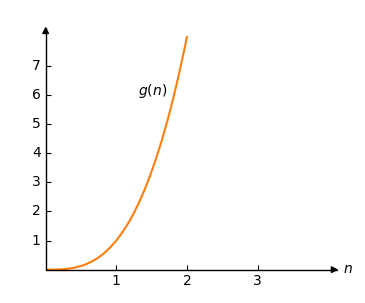
使用大 O 符號,我們可以說 \(O(g(n))\) 是 \(f(n)\) 的上界,因為我們可以選擇一個常數 \(C \),使得只要 \(n \) 足夠大,就有 \(C \cdot g(n)>f(n)\)。
好的,讓我們試試。我們選擇 \(C=0.75 \),這樣 \(C \cdot g(n) = 0.75 \cdot n^3\)。
現在,讓我們在同一個圖中繪製 \(0.75 \cdot g(n)\) 和 \(f(n)\)
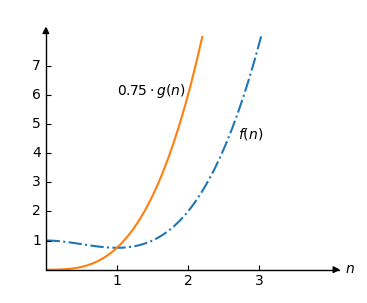
我們可以看到 \(O(g(n))=O(n^3)\) 是 \(f(n)\) 的上界,因為對於所有大於 1 的 \(n \),都有 \(0.75 \cdot g(n) > f(n)\)。
在上面的例子中,\(n\) 必須大於 1 才能使 \(O(n^3)\) 成為上界。我們將這個限制稱為 \(n_0\)。
Definition(定義)
設 \(f(n)\) 和 \(g(n)\) 為兩個函式。我們說 \(f(n)\) 是 \(O(g(n))\) 當且僅當存在正的常數 \(C\) 和 \(n_0\),使得
\[ C \cdot g(n) > f(n) \]
對於所有 \(n>n_0\)。
在評估演算法的時間複雜度時,\(O()\)
只對大量 \(n \) 值有效是可以的,因為這正是時間複雜度變得重要的時候。換句話說:如果我們正在排序,10、20 或 100 個值,演算法的時間複雜度並不是那麼有趣,因為計算機無論如何都會在短時間內對這些值進行排序。

