DSA 二分查詢

二分查詢

二分查詢演算法透過在一個數組中搜索並返回其查詢值的索引。

執行模擬，看看二分查詢演算法是如何工作的。

要檢視當找不到某個值時會發生什麼，請嘗試查詢值 5。

二分查詢比線性查詢快得多，但需要一個已排序的陣列才能工作。

二分查詢演算法透過檢查陣列中間的值來工作。如果目標值較小，則下一個要檢查的值位於陣列左半部分的中心。這種搜尋方式意味著搜尋區域始終是前一個搜尋區域的一半，這就是二分查詢演算法如此之快的原因。

這個將搜尋區域減半的過程一直持續到找到目標值，或者直到陣列的搜尋區域為空。

手動演練

讓我們手動嘗試一下搜尋過程，以便在實際用程式語言實現之前，能更清楚地理解二分查詢是如何工作的。我們將搜尋值 11。

步驟 1: 我們從一個數組開始。

步驟 2: 陣列中索引為 3 的中間值，它等於 11 嗎？

步驟 3: 7 小於 11，所以我們必須在索引 3 的右側搜尋 11。索引 3 右側的值為 [ 11, 15, 25]。下一個要檢查的值是中間值 15，位於索引 5。

步驟 4: 15 大於 11，所以我們必須在索引 5 的左側搜尋。我們已經檢查了索引 0-3，因此只有索引 4 還有值需要檢查。

我們找到了！

在索引 4 處找到值 11。

返回索引位置 4。

二分查詢完成。

執行下面的模擬，以動畫形式檢視以上步驟。

手動執行：發生了什麼？

起初，演算法有兩個變數“left”和“right”。

“left”為 0，表示陣列中第一個值的索引，“right”為 6，表示陣列中最後一個值的索引。

\((left+right)/2=(0+6)/2=3\) 是用於檢查中間值（7）是否等於目標值（11）的第一個索引。

7 小於目標值 11，因此在下一個迴圈中，搜尋區域必須限制在中間值的右側：[ 11, 15, 25]，位於索引 4-6。

為了限制搜尋區域並找到一個新的中間值，“left”更新為索引 4，“right”仍然是 6。4 和 6 是新搜尋區域的第一個和最後一個值的索引，即前一箇中間值的右側。新的中間值索引是 \((left+right)/2=(4+6)/2=10/2=5\)。

檢查索引 5 處的新中間值：15 大於 11，所以如果目標值 11 存在於陣列中，它必定在索引 5 的左側。新搜尋區域是透過將“right”從 6 更新為 4 來建立的。現在，“left”和“right”都是 4，\((left+right)/2=(4+4)/2=4\)，因此只剩下索引 4 需要檢查。在索引 4 處找到目標值 11，因此返回索引 4。

總而言之，二分查詢演算法就是透過不斷地將陣列搜尋區域減半，直到找到目標值。

當找到目標值時，將返回目標值的索引。如果未找到目標值，則返回 -1。

二分查詢實現

要實現二分查詢演算法，我們需要

1. 一個包含要搜尋值的陣列。
2. 一個要搜尋的目標值。
3. 一個只要 left 索引小於或等於 right 索引就一直執行的迴圈。
4. 一個 if 語句，用於比較中間值與目標值，並在找到目標值時返回索引。
5. 一個 if 語句，用於檢查目標值是否小於或大於中間值，並更新“left”或“right”變數以縮小搜尋區域。
6. 迴圈結束後，返回 -1，因為此時我們知道目標值未找到。

二分查詢的結果程式碼如下：

def binarySearch(arr, targetVal):
    left = 0
    right = len(arr) - 1

    while left <= right:
        mid = (left + right) // 2

        if arr[mid] == targetVal:
            return mid
        
        if arr[mid] < targetVal:
            left = mid + 1
        else:
            right = mid - 1

    return -1

myArray = [1, 3, 5, 7, 9, 11, 13, 15, 17, 19]
myTarget = 15

result = binarySearch(myArray, myTarget)

if result != -1:
    print("Value",myTarget,"found at index", result)
else:
    print("Target not found in array.")

二分查詢時間複雜度

有關時間複雜度的一般性解釋，請訪問此頁面。

有關插入排序時間複雜度的更全面詳細的解釋，請訪問此頁面。

每次二分查詢檢查一個新值以確定它是否是目標值時，搜尋區域都會減半。

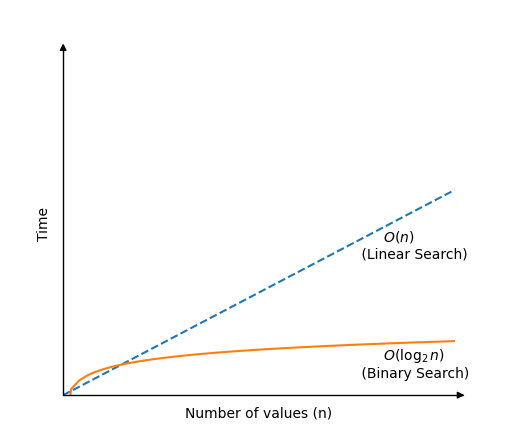
這意味著，即使在最壞的情況下，二分查詢也找不到目標值，它仍然只需要 \( \log_{2}n \) 次比較即可搜尋完一個包含 \(n\) 個值的已排序陣列。

二分查詢的時間複雜度是

\[ O( \log_{2} n ) \]

如果我們畫出二分查詢在包含 \(n\) 個值的陣列中查詢值所需的時間與線性查詢的比較圖，我們會得到這張圖

執行下面的二分查詢模擬，使用不同數量的值 \(n\) 的陣列，並觀察二分查詢需要多少次比較才能找到目標值

正如你在執行二分查詢模擬時所看到的，即使陣列很大且我們正在尋找的值未找到，搜尋也只需要很少的比較。

For the Binary Search algorithm to work,
the array must already be .