DSA 線性搜尋時間複雜度

有關時間複雜度的通用解釋，請參閱此頁面。

線性搜尋時間複雜度

有關時間複雜度的一般性解釋，請訪問此頁面。

有關插入排序時間複雜度的更全面、詳細的解釋，請訪問 此頁面。

線性搜尋 將每個值與要查詢的值進行比較。如果找到該值，則返回其索引；如果未找到，則返回 -1。

要找出線性搜尋的時間複雜度，讓我們看看在包含 \(n\) 個值的陣列中查詢值所需的比較操作次數。

最佳情況場景是，如果我們正在查詢的值是陣列中的第一個值。在這種情況下，只需一次比較，時間複雜度為 \(O(1)\)。

最壞情況場景是，在不找到目標值的情況下，整個陣列都被搜尋過。在這種情況下，陣列中的所有值都與目標值進行了比較，時間複雜度為 \(O(n)\)。

平均情況場景並不容易確定。找到目標值的可能性有多大？這取決於陣列中的值，對吧？但如果我們假設陣列中的一個值等於目標值，並且該值的位置可以是任意的，那麼線性搜尋所需的平均時間是比最壞情況場景所需時間的一半。

線性搜尋的時間複雜度為 \(O(n)\)。

如果我們繪製線性搜尋在包含 \(n\) 個值的陣列中查詢值所需時間的圖表，我們會得到這個圖：

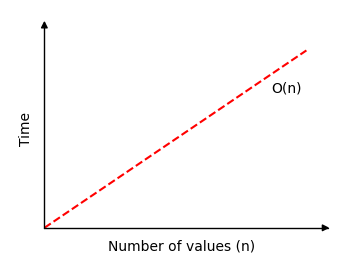
線性搜尋模擬

執行不同數量值的陣列的模擬，看看線性搜尋找到 \(n\) 個值陣列中的值需要多少次比較。

正如你在執行線性搜尋模擬時所看到的，如果值很快就被找到，搜尋只需要很少的比較，但如果我們正在尋找的值沒有被找到，那麼就會進行最多的比較。