一個簡單的演算法

斐波那契數列

斐波那契數列在介紹演算法方面非常有用，所以在我們繼續之前，先簡要介紹一下斐波那契數列。

斐波那契數列是以一位名叫斐波那契的 13 世紀義大利數學家命名的。

前兩個斐波那契數是 0 和 1，下一個斐波那契數始終是前兩個數的和，因此我們得到 0、1、1、2、3、5、8、13、21、...

本教程將大量使用迴圈和遞迴。所以在我們繼續之前，讓我們來實現三個不同版本的演算法來建立斐波那契數，以簡單的方式展示迴圈程式設計和遞迴程式設計的區別。

斐波那契數演算法

要生成一個斐波那契數，我們只需要將前兩個斐波那契數相加。

斐波那契數列是展示演算法是什麼的一個好方法。我們知道如何找到下一個數字的原理，所以我們可以編寫一個演算法來生成儘可能多的斐波那契數。

下面是生成前 20 個斐波那契數的演算法。

迴圈與遞迴

為了展示迴圈和遞迴的區別，我們將實現三種不同的方法來找出斐波那契數

1. 上面斐波那契演算法的實現，使用 for 迴圈。
2. 上面斐波那契演算法的實現，使用遞迴。
3. 使用遞迴找出第 \(n\) 個斐波那契數。

1. 使用 For 迴圈實現

在編寫程式碼之前，列出程式碼必須包含或執行的內容可能是一個好主意

• 兩個變數來儲存前兩個斐波那契數
• 一個迴圈 18 次的 for 迴圈
• 透過將前兩個數相加來建立新的斐波那契數
• 列印新的斐波那契數
• 更新儲存前兩個斐波那契數的變數

使用上面的列表，編寫程式會更容易

prev2 = 0
prev1 = 1

print(prev2)
print(prev1)
for fibo in range(18):
    newFibo = prev1 + prev2
    print(newFibo)
    prev2 = prev1
    prev1 = newFibo

2. 使用遞迴實現

遞迴是指一個函式呼叫自身。

要實現斐波那契演算法，我們需要與上面的程式碼示例中的大多數相同的內容，但我們需要用遞迴替換 for 迴圈。

要用遞迴替換 for 迴圈，我們需要將大部分程式碼封裝在一個函式中，並且需要該函式呼叫自身來建立新的斐波那契數，只要生成的斐波那契數數量低於或等於 19。

我們的程式碼如下

print(0)
print(1)
count = 2

def fibonacci(prev1, prev2):
    global count
    if count <= 19:
        newFibo = prev1 + prev2
        print(newFibo)
        prev2 = prev1
        prev1 = newFibo
        count += 1
        fibonacci(prev1, prev2)
    else:
        return

fibonacci(1,0)

3. 使用遞迴找出第 \(n\) 個斐波那契數

要找出第 \(n\) 個斐波那契數，我們可以根據斐波那契數 \(n\) 的數學公式編寫程式碼

\[F(n) = F(n-1) + F(n-2) \]

這只是意味著，例如，第 10 個斐波那契數是第 9 個和第 8 個斐波那契數的和。

在使用遞迴的概念時，我們可以讓函式呼叫自身，只要 \(n\) 小於或等於 1。如果 \(n \le 1\)，則意味著程式碼執行已達到第一個斐波那契數 1 或 0。

程式碼如下

def F(n):
    if n <= 1:
        return n
    else:
        return F(n - 1) + F(n - 2)

print(F(19))

請注意，此遞迴方法呼叫自身兩次，而不僅僅是一次。這會極大地影響程式在計算機上的實際執行方式。當我們增加我們想要的斐波那契數的數量時，計算量將呈指數級增長。更具體地說，當我們想要的斐波那契數增加一倍時，函式呼叫的數量也將翻倍。

看看 \(F(5)\) 的函式呼叫次數

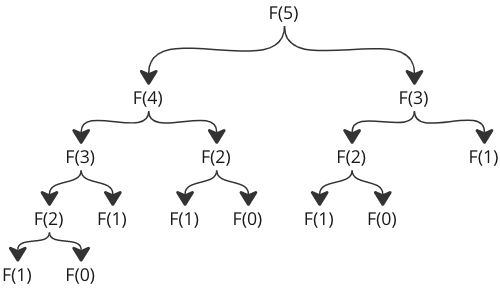
為了更好地理解程式碼，這裡是遞迴函式如何返回值的示例，以便 \(F(5)\) 最終返回正確的值

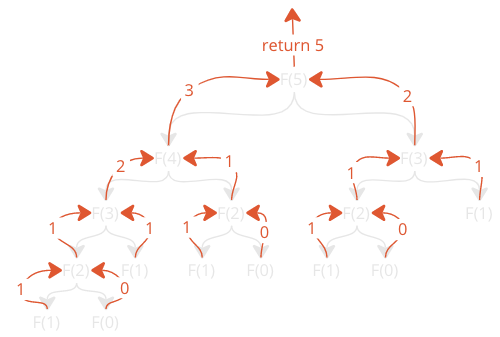
這裡有兩個重要的事情需要注意：函式呼叫的數量，以及函式被相同引數呼叫的次數。

因此，儘管程式碼很吸引人並且展示了遞迴的工作方式，但實際的程式碼執行對於生成大的斐波那契數來說太慢且效率低下。

總結

在我們繼續之前，讓我們回顧一下我們到目前為止看到的內容

• 演算法可以在不同的程式語言中以不同的方式實現。
• 遞迴和迴圈是可用於實現演算法的兩種不同的程式設計技術。

現在是時候繼續研究我們將要看的第一個資料結構：陣列。

點選“下一篇”按鈕繼續。

print(0)
print(1)
count = 2

def fibonacci(prev1, prev2):
    global count
    if count <= 19:
        newFibo = prev1 + prev2
        print(newFibo)
        prev2 = prev1
        prev1 = newFibo
        count += 1
        (prev1, prev2)
    else:
        return

fibonacci(1,0)