DSA 計數排序

計數排序

計數排序演算法透過計算每個值出現的次數來對陣列進行排序。

執行模擬，看看如何使用計數排序對 1 到 5 之間的 17 個整數值進行排序。

計數排序不像我們之前看過的其他排序演算法那樣進行值比較，它只適用於非負整數。

此外，當可能值的範圍 \(k\) 小於值的數量 \(n\) 時，計數排序非常快。

計數排序的條件

這些是計數排序被認為僅適用於有限範圍的非負整數值的原因

• 整數值：計數排序依賴於對不同值出現次數的計數，因此它們必須是整數。對於整數，每個值都可以與一個索引匹配（對於非負值），並且存在有限數量的不同值，因此可能的不同值 \(k\) 的數量不會比值的數量 \(n\) 大太多。
• 非負值：計數排序通常透過建立計數陣列來實現。當演算法遍歷需要排序的值時，透過增加計數陣列中索引 x 處的值來計算值 x。如果我們嘗試對負值進行排序，那麼對於值 -3，我們會遇到麻煩，因為索引 -3 將在計數陣列之外。
• 值的範圍有限：如果可能要排序的不同值的數量 \(k\) 大於要排序的值的數量 \(n\)，那麼我們排序所需的計數陣列將大於我們擁有的需要排序的原始陣列，演算法會變得無效。

手動演練

在用程式語言實現計數排序演算法之前，讓我們手動遍歷一個短陣列，以便先了解其思路。

步驟 1：我們從一個未排序的陣列開始。

步驟 2：我們建立另一個數組來統計每個值的數量。該陣列有 4 個元素，用於儲存 0 到 3 的值。

步驟 3：現在我們開始計數。第一個元素是 2，所以我們必須將計數陣列索引 2 處的元素加一。

步驟 4：計數完一個值後，我們可以將其移除，然後計數下一個值，即 3。

步驟 5：我們計數的下一個值是 0，所以我們將計數陣列索引 0 處的元素加一。

步驟 6：我們繼續這樣做，直到所有值都被計數。

步驟 7：現在我們將從初始陣列中重新建立元素，並且我們將按從小到大的順序進行。

計數陣列中的第一個元素告訴我們有一個值為 0 的元素。因此，我們將一個值為 0 的元素新增到陣列中，並將計數陣列索引 0 處的元素減一。

步驟 8：從計數陣列中，我們看到我們不需要建立值為 1 的元素。

步驟 9：我們將 3 個值為 2 的元素新增到陣列末尾。在我們建立這些元素的同時，我們也減少了計數陣列索引 2 處的值。

步驟 10：最後，我們必須在陣列末尾新增 2 個值為 3 的元素。

終於！陣列已排序。

執行下面的模擬，以動畫形式檢視以上步驟。

手動執行：發生了什麼？

在用程式語言實現演算法之前，我們需要更詳細地回顧一下上面發生的事情。

我們已經看到計數排序演算法分兩個步驟進行

1. 每個值都透過在計數陣列的正確索引處遞增來計數。計數完一個值後，它就會被移除。
2. 值透過使用計數陣列中的計數和計數索引，以正確的順序重新建立。

有了這個想法，我們就可以開始使用 Python 來實現演算法了。

計數排序實現

要在程式語言中實現計數排序演算法，我們需要

1. 一個包含待排序值的陣列。
2. 一個接收整數陣列的“countingSort”方法。
3. 方法內部的一個數組，用於儲存值的計數。
4. 方法內部的一個迴圈，透過遞增計數陣列中的元素來計數和移除值。
5. 方法內部的一個迴圈，透過使用計數陣列來重新建立陣列，使元素按正確的順序出現。

還有一件事：我們需要找出陣列中的最大值，這樣計數陣列才能以正確的尺寸建立。例如，如果最大值為 5，那麼計數陣列必須總共有 6 個元素，才能計數所有可能的非負整數 0、1、2、3、4 和 5。

生成的程式碼如下：

def countingSort(arr):
    max_val = max(arr)
    count = [0] * (max_val + 1)

    while len(arr) > 0:
        num = arr.pop(0)
        count[num] += 1

    for i in range(len(count)):
        while count[i] > 0:
            arr.append(i)
            count[i] -= 1

    return arr

unsortedArr = [4, 2, 2, 6, 3, 3, 1, 6, 5, 2, 3]
sortedArr = countingSort(unsortedArr)
print("Sorted array:", sortedArr)

計數排序時間複雜度

有關時間複雜度的一般性解釋，請訪問此頁面。

有關插入排序時間複雜度的更全面詳細的解釋，請訪問此頁面。

計數排序演算法的執行速度取決於可能值的範圍 \(k\) 和值的數量 \(n\)。

總的來說，計數排序的時間複雜度為 \(O(n+k)\)。

在最佳情況下，可能的不同值的範圍 \(k\) 相對於值的數量 \(n\) 非常小，計數排序的時間複雜度為 \(O(n)\)。

但在最壞的情況下，可能的不同值的範圍 \(k\) 相對於值的數量 \(n\) 非常大，計數排序的時間複雜度可能為 \(O(n^2)\) 甚至更糟。

下面的圖顯示了計數排序的時間複雜度可能變化多大。

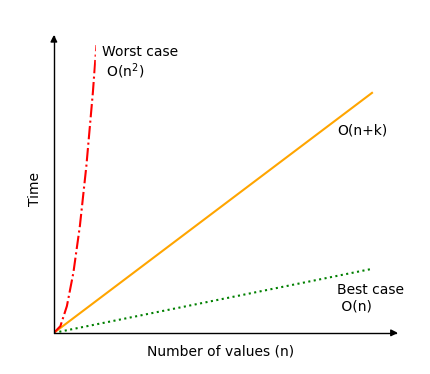
如您所見，在選擇計數排序作為演算法之前，考慮值的範圍與要排序的值的數量進行比較非常重要。另外，正如頁面頂部提到的，請記住，計數排序僅適用於非負整數值。

執行計數排序的不同模擬，以檢視操作次數如何落在最壞情況 \(O(n^2)\)（紅線）和最佳情況 \(O(n)\)（綠線）之間。

如前所述：如果待排序的數字值差異很大（\(k\) 很大），而要排序的數字很少（\(n\) 很小），則計數排序演算法效果不佳。

如果我們保持 \(n\) 和 \(k\) 固定，“隨機”、“降序”和“升序”選項在上面的模擬中導致的操作次數相同。這是因為在這三種情況下都會發生相同的事情：設定計數陣列，對數字進行計數，然後建立新的排序後的陣列。

[,,,4,2,1]