DSA 基數排序時間複雜度

有關時間複雜度的通用解釋，請參閱此頁面。

基數排序時間複雜度

基數排序演算法一次對非負整數進行一位排序。

需要排序的值有 \(n\) 個，而 \(k\) 是最高值中的位數。

當基數排序執行時，每個值都會被移入基數陣列，然後再移回初始陣列。所以 \(n\) 個值被移入基數陣列，\(n\) 個值被移回。這給了我們 \(n + n = 2 \cdot n\) 次操作。

而上述移動值的操作需要針對每一位數字進行。這使得我們總共有 \(2 \cdot n \cdot k\) 次操作。

這使得基數排序的時間複雜度為

\[ O(2 \cdot n \cdot k) = \underline{\underline{O(n \cdot k)}} \]

只要位數 \(k\) 相對於值的數量 \(n\) 保持相對較小，基數排序可能是最快的排序演算法之一。

我們可以設想一種情況，即位數 \(k\) 與值的數量 \(n\) 相同，在這種情況下，我們得到時間複雜度 \(O(n \cdot k)=O(n^2)\)，這相當慢，並且與氣泡排序等演算法具有相同的時間複雜度。

我們還可以設想一種情況，即位數 \(k\) 隨著值的數量 \(n\) 的增長而增長，即 \(k(n)= \log n\)。在這種情況下，我們得到時間複雜度 \(O(n \cdot k)=O(n \cdot \log n )\)，這與快速排序等演算法相同。

參見下圖中的基數排序時間複雜度。

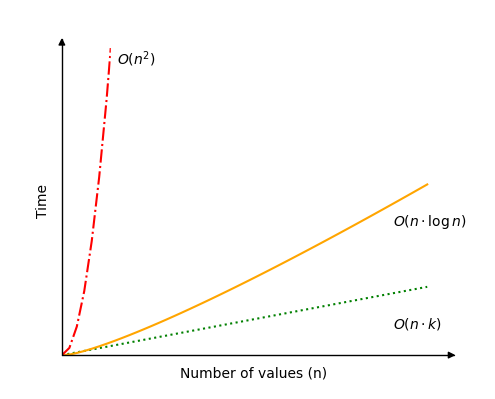
基數排序模擬

執行不同的基數排序模擬，以瞭解操作次數如何落在最壞情況 \(O(n^2)\)（紅線）和最佳情況 \(O(n)\)（綠線）之間。

表示不同值的條形被縮放以適應視窗，使其看起來正常。這意味著具有 7 位數的值看起來只比具有 2 位數的值大 5 倍，但實際上，具有 7 位數的值實際上比具有 2 位數的值大 5000 倍！

如果我們保持 \(n\) 和 \(k\) 固定，上面模擬中的“隨機”、“降序”和“升序”選項會導致相同數量的操作。這是因為在所有三種情況下都會發生相同的事情。