DSA 氣泡排序時間複雜度

有關時間複雜度的通用解釋，請參閱上一頁。

氣泡排序時間複雜度

氣泡排序演算法在最壞情況下需要對長度為 \(n\) 的陣列進行 \(n-1\) 次遍歷。

第一次遍歷時，演算法會將每個元素與下一個元素進行比較，如果左邊的值大於右邊的值，則交換它們。這意味著最大的值會“冒泡”到最後，並且未排序的陣列部分會越來越短，直到排序完成。因此，在平均情況下，當演算法遍歷陣列進行比較和交換值時，會考慮 \(\frac{n}{2}\) 個元素。

我們可以開始計算氣泡排序演算法對 \(n\) 個值的操作次數：

\[操作次數 = (n-1)\cdot \frac{n}{2} = \frac{n^2}{2} - \frac{n}{2} \]

在考慮演算法的時間複雜度時，我們關注非常大的資料集，這意味著 \(n\) 是一個非常大的數字。對於一個非常大的數字 \(n\)，\(\frac{n^2}{2}\) 項會比 \(\frac{n}{2}\) 項大得多。大到我們可以透過簡單地移除第二項 \(\frac{n}{2}\) 來進行近似。

\[操作次數 = \frac{n^2}{2} - \frac{n}{2} \approx \frac{n^2}{2} = \frac{1}{2} \cdot n^2 \]

當我們在這裡使用大 O 符號來分析時間複雜度時，因子會被忽略，因此 \(\frac{1}{2}\) 這個因子會被省略。這意味著氣泡排序演算法的執行時間可以使用大 O 符號來描述，如下所示：

\[ O( \frac{1}{2} \cdot n^2) = \underline{\underline{O(n^2)}} \]

描述氣泡排序時間複雜度的圖如下所示：

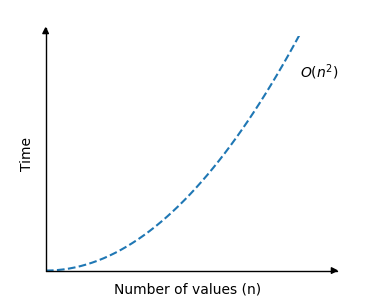
正如你所見，當陣列大小增加時，執行時間會非常快地增加。

幸運的是，有一些排序演算法比它更快，例如 快速排序。

氣泡排序模擬

選擇陣列中的元素數量，然後執行此模擬，以瞭解氣泡排序處理 \(n\) 個元素的陣列所需的操作次數 \(O(n^2)\)。

上方的紅線表示上限時間複雜度 \(O(n^2)\)，而此時的實際函式是 \(1.05 \cdot n^2\)。

如果存在一個正常量 \(C\)，使得對於大量的 \(n\) 值，\(C \cdot g(n) > f(n)\)，則稱函式 \(f(n)\) 為 \(O(g(n))\)。

在這種情況下，\(f(n)\) 是氣泡排序使用的運算元，\(g(n)=n^2\)，\(C=1.05\)。

在此頁面上閱讀更多關於大 O 符號和時間複雜度的資訊。