DSA 選擇排序
選擇排序
選擇排序演算法查詢陣列中的最小值,並將其移到陣列的前面。
速度
{{ msgDone }}該演算法一遍又一遍地查詢陣列,將下一個最小值移到前面,直到陣列被排序。
工作原理
- 遍歷陣列以查詢最小值。
- 將最小值移到未排序部分的前面。
- 再遍歷陣列,次數與陣列中的值數量相同。
繼續閱讀,以完全理解選擇排序演算法以及如何自己實現它。
手動演練
在用程式語言實現選擇排序演算法之前,讓我們只進行一次手動遍歷一個短陣列,以獲得一些想法。
步驟 1:我們從一個未排序的陣列開始。
[ 7, 12, 9, 11, 3]
步驟 2:逐個遍歷陣列。哪個值是最小的? 3,對嗎?
[ 7, 12, 9, 11, 3]
步驟 3:將最小值 3 移到陣列的前面。
[ 3, 7, 12, 9, 11]
步驟 4:檢視剩餘的值,從 7 開始。 7 是最小的值,並且已經放在了陣列的前面,所以我們不需要移動它。
[ 3, 7, 12, 9, 11]
步驟 5:檢視陣列的其餘部分:12、9 和 11。 9 是最小值。
[ 3, 7, 12, 9, 11]
步驟 6:將 9 移到前面。
[ 3, 7, 9, 12, 11]
步驟 7:檢視 12 和 11,11 是最小的。
[ 3, 7, 9, 12, 11]
步驟 8:將其移到前面。
[ 3, 7, 9, 11, 12]
最後,陣列已排序。
執行下面的模擬,以動畫形式檢視以上步驟。
手動執行:發生了什麼?
我們必須理解上面發生了什麼,才能完全理解該演算法,以便用程式語言實現該演算法。
您能看出最小值 3 發生了什麼嗎?在步驟 3 中,它已被移到陣列的開頭,這是它應在的位置,但在該步驟中,陣列的其餘部分仍未排序。
因此,選擇排序演算法必須一遍又一遍地遍歷陣列,每次都將下一個最小值移到未排序部分的前面,移到其正確的位置。排序一直進行到最大值 12 留在陣列末尾。這意味著我們需要遍歷陣列 4 次,以對 5 個值的陣列進行排序。
每次演算法遍歷陣列時,陣列中剩餘的未排序部分都會變短。
現在,我們將使用我們學到的知識來實現程式語言中的選擇排序演算法。
選擇排序實現
要在程式語言中實現選擇排序演算法,我們需要
- 一個包含待排序值的陣列。
- 一個內迴圈,遍歷陣列,找到最小值,並將其移到陣列的前面。此迴圈每次執行時必須少迴圈一個值。
- 一個外迴圈,控制內迴圈需要執行多少次。對於具有 \(n\) 個值的陣列,此外迴圈必須執行 \(n-1\) 次。
生成的程式碼如下:
示例
my_array = [64, 34, 25, 5, 22, 11, 90, 12]
n = len(my_array)
for i in range(n-1):
min_index = i
for j in range(i+1, n):
if my_array[j] < my_array[min_index]:
min_index = j
min_value = my_array.pop(min_index)
my_array.insert(i, min_value)
print("Sorted array:", my_array)選擇排序移動問題
選擇排序演算法可以進一步改進。
在上面的程式碼中,移除了最小值的元素,然後將其插入到陣列的前面。
每次刪除下一個最小值的陣列元素時,所有後續元素都必須向下移動一個位置以彌補刪除。
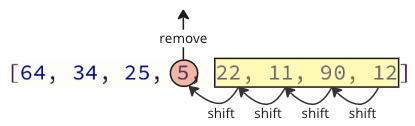
這些移動操作花費了大量時間,而且我們還沒有完成!找到並移除了最小值(5)之後,將其插入到陣列的開頭,導致所有後續值移動一個位置以騰出新值空間,如下圖所示。
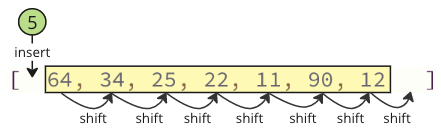
注意:如果您使用的是 Python 或 Java 等高階程式語言,則在程式碼中不會看到這些移動操作,但移動操作仍在後臺進行。這些移動操作需要計算機額外的時間來完成,這可能是一個問題。
解決方案:交換值!
而不是所有的移動,而是像下圖所示那樣,將最小值(5)與第一個值(64)進行交換。

我們可以像上圖所示那樣交換值,因為最小值最終會到達正確的位置,而我們與之交換的其他值的位置並不重要,因為它還沒有排序。
這是一個模擬,顯示了這種改進的選擇排序如何透過交換工作
速度
{{ msgDone }}這是改進的選擇排序的實現,使用了交換
示例
my_array = [64, 34, 25, 12, 22, 11, 90, 5]
n = len(my_array)
for i in range(n):
min_index = i
for j in range(i+1, n):
if my_array[j] < my_array[min_index]:
min_index = j
my_array[i], my_array[min_index] = my_array[min_index], my_array[i]
print("Sorted array:", my_array)選擇排序時間複雜度
有關時間複雜度的一般性解釋,請訪問此頁面。
有關選擇排序時間複雜度的更全面、更詳細的解釋,請訪問此頁面。
選擇排序對 \(n\) 個值的陣列進行排序。
平均而言,大約 \(\frac{n}{2}\) 個元素需要進行比較才能在每次迴圈中找到最小值。
並且選擇排序大約需要執行 \(n\) 次迴圈來查詢最小值。
我們得到時間複雜度
\[ O( \frac{n}{2} \cdot n) = \underline{\underline{O(n^2)}} \]
選擇排序演算法的時間複雜度可以在圖表中顯示如下
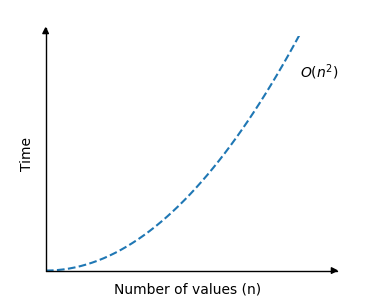
正如您所見,執行時間與氣泡排序相同:當陣列大小增加時,執行時間增加得非常快。
為不同大小的陣列執行下面的模擬。
紅色虛線代表理論時間複雜度 \(O(n^2)\)。
藍色十字出現在您執行模擬時。藍色十字顯示了對給定大小的陣列進行排序所需的運算次數。
{{ this.userX }}
操作次數:{{ operations }}
與氣泡排序相比,我們在此模擬中注意到的最顯著的區別是,對於選擇排序,最佳情況和最壞情況實際上幾乎相同(\(O(n^2)\)),但對於氣泡排序,最佳情況的執行時間僅為 \(O(n)\)。
選擇排序的最佳情況和最壞情況之間的差異主要是交換次數。在最佳情況下,選擇排序不必交換任何值,因為陣列已經排序。而在最壞情況下,陣列已經排序,但順序錯誤,因此選擇排序必須進行與陣列中值一樣多的交換。

