DSA 特定演算法的時間複雜度

有關時間複雜度的通用解釋，請參閱此頁面。

快速排序時間複雜度

快速排序演算法選擇一個值作為“樞軸”元素，並將其他值移動，使大於樞軸的值位於樞軸元素的右側，小於樞軸的值位於樞軸元素的左側。

然後，快速排序演算法透過遞迴地對樞軸元素左右兩側的子陣列進行排序，直到陣列被排序。

最壞情況

要找到快速排序的時間複雜度，我們可以從最壞情況開始分析。

快速排序的最壞情況是陣列已經排序。在這種情況下，每次遞迴呼叫後只有一個子陣列，並且新子陣列比前一個數組短一個元素。

這意味著快速排序必須遞迴呼叫自身 \(n\) 次，並且每次都必須進行 \(\frac{n}{2}\) 次平均比較。

最壞情況時間複雜度為：

\[ O(n \cdot \frac{n}{2}) = \underline{\underline{O(n^2)}} \]

平均情況

平均而言，快速排序實際上要快得多。

快速排序在平均情況下速度很快，因為每次快速排序遞迴執行時，陣列大約被分成兩半，所以子陣列的大小減小得非常快，這意味著不需要太多遞迴呼叫，並且快速排序可以比最壞情況更快地完成。

下圖顯示了用快速排序對包含 23 個值的陣列進行排序時，陣列是如何被分成子陣列的。

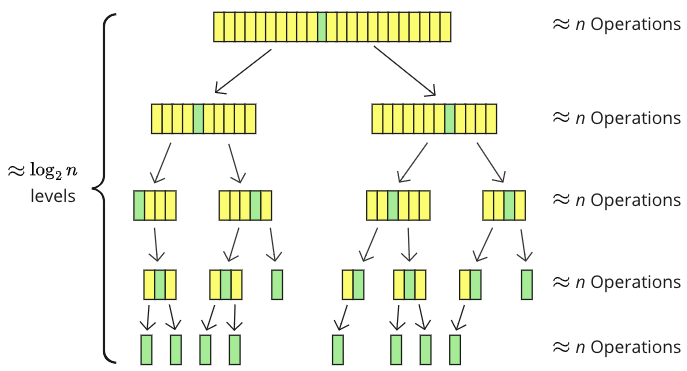
樞軸元素（綠色）被移到中間，陣列被分成子陣列（黃色）。有 5 個遞迴級別，子陣列越來越小，每個級別大約有 \(n\) 個值以某種方式被觸及：比較、移動或兩者都進行。

\( \log_2 \) 表示一個數字可以分成 2 的次數，所以 \( \log_2 \) 是遞迴級別的數量的一個很好的估計。 \( \log_2(23) \approx 4.5 \)，這對於上面具體示例中的遞迴級別數量來說是一個足夠好的近似值。

實際上，子陣列並不總是精確地分成兩半，並且每個級別並不總是比較或移動 \(n\) 個值，但我們可以說這是計算時間複雜度的平均情況。

\[ \underline{\underline{O(n \cdot \log_2n)}} \]

下面您可以看到與之前的排序演算法（氣泡排序、選擇排序和插入排序）相比，快速排序在平均情況下的時間複雜度的顯著改進。

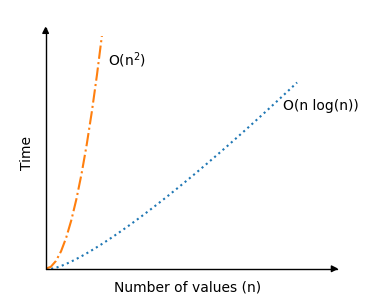
快速排序演算法的遞迴部分實際上是平均排序場景如此之快的原因，因為對於樞軸元素的良好選擇，陣列將在演算法每次呼叫自身時大致均勻地分成兩半。因此，即使 \(n\) 的數量翻倍，遞迴呼叫的次數也不會翻倍。

快速排序模擬

使用下面的模擬來檢視理論時間複雜度 \(O(n^2)\)（紅線）與實際快速排序執行的運算元量的比較。

上圖中的紅線代表最壞情況下的理論上限時間複雜度 \(O(n^2)\)，綠線代表具有隨機值的平均情況時間複雜度 \(O(n \log_2n)\)。

對於快速排序，平均隨機情況和已排序陣列的情況之間存在很大差異。您可以透過執行上面的不同模擬來看到這一點。

升序排序的陣列需要大量操作的原因在於，由於其實現方式，它需要最多的元素交換。在這種情況下，選擇最後一個元素作為樞軸元素，而最後一個元素也是最大的數字。因此，每個子陣列中的所有其他值都會被交換到樞軸元素的左側（它們已經位於該位置）。