DSA 插入排序

插入排序

插入排序演算法使用陣列的一部分來儲存已排序的值，另一部分儲存尚未排序的值。

演算法一次從陣列的未排序部分取出一個值，並將其放到已排序部分陣列中的正確位置，直到陣列被排序。

繼續閱讀，以完全理解插入排序演算法以及如何自己實現它。

手動演練

在用程式語言實現插入排序演算法之前，我們先手動走一遍一個短陣列，以便獲得一些概念。

步驟 1：我們從一個未排序的陣列開始。

步驟 2: 我們可以將第一個值視為陣列的初始排序部分。如果只有一個值，那它肯定是有序的，對吧？

步驟 3: 下一個值 12 現在應該移動到已排序部分陣列中的正確位置。但是 12 大於 7，所以它已經在正確的位置上。

步驟 4: 考慮下一個值 9。

步驟 5: 值 9 現在必須移動到已排序部分陣列中的正確位置，所以我們將 9 放在 7 和 12 之間。

步驟 6: 下一個值是 11。

步驟 7: 我們將其移到已排序部分陣列中的 9 和 12 之間。

步驟 8: 要插入到正確位置的最後一個值是 3。

步驟 9: 我們將 3 放在所有其他值的前面，因為它是最低的值。

最終，陣列已排序。

執行下面的模擬，以動畫形式檢視以上步驟。

手動執行：發生了什麼？

我們必須理解上面發生的一切，才能完全理解該演算法，以便我們能夠用程式語言實現該演算法。

第一個值被視為陣列的初始排序部分。

第一個值之後的所有值都必須與演算法已排序部分中的值進行比較，以便將其插入到正確的位置。

插入排序演算法必須遍歷陣列 4 次，以排序包含 5 個值的陣列，因為我們不必對第一個值進行排序。

每次演算法遍歷陣列時，陣列中剩餘的未排序部分都會變短。

我們現在將使用我們學到的知識來實現程式語言中的插入排序演算法。

插入排序實現

要在程式語言中實現插入排序演算法，我們需要

1. 一個包含待排序值的陣列。
2. 一個外層迴圈，用於選擇一個要排序的值。對於一個包含 \(n\) 個值的陣列，這個外層迴圈跳過第一個值，並且必須執行 \(n-1\) 次。
3. 一個內層迴圈，用於遍歷已排序部分陣列，以找到要插入該值的位置。如果要排序的值位於索引 \(i\) 處，則陣列的已排序部分從索引 \(0\) 開始，到索引 \(i-1\) 結束。

生成的程式碼如下：

my_array = [64, 34, 25, 12, 22, 11, 90, 5]

n = len(my_array)
for i in range(1,n):
    insert_index = i
    current_value = my_array.pop(i)
    for j in range(i-1, -1, -1):
        if my_array[j] > current_value:
            insert_index = j
    my_array.insert(insert_index, current_value)

print("Sorted array:", my_array)

插入排序改進

插入排序可以進一步改進。

上面程式碼中先刪除一個值然後將其插入到另一個位置的方式是很直觀的。例如，如果你用手牌來做插入排序，你就會這樣做。如果將低數值的牌按順序排在左邊，你拿起一張新的未排序的牌，然後將其插入到已排序牌的正確位置。

這種程式設計方式的問題在於，當從陣列中刪除一個值時，所有上面的元素都必須向下移動一個索引位

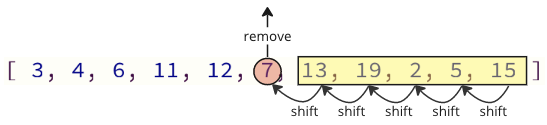
並且當再次將移除的值插入到陣列中時，也有許多移位操作必須完成：所有後續元素都必須向上移動一個位置，以為插入的值騰出空間

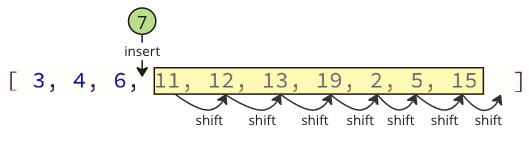
這些移位操作可能會花費大量時間，特別是對於包含許多元素的陣列。

改進的解決方案

我們可以透過只移動必要的值來避免大部分的移位操作

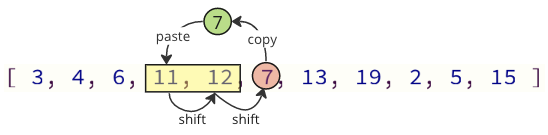
在上面的圖中，首先複製了值 7，然後將值 11 和 12 向上移動一位，最後將值 7 放在原來值 11 的位置。

在這種情況下，移位操作的數量從 12 減少到 2。

下面的示例實現了這一改進

my_array = [64, 34, 25, 12, 22, 11, 90, 5]

n = len(my_array)
for i in range(1,n):
    insert_index = i
    current_value = my_array[i]
    for j in range(i-1, -1, -1):
        if my_array[j] > current_value:
            my_array[j+1] = my_array[j]
            insert_index = j
        else:
            break
    my_array[insert_index] = current_value

print("Sorted array:", my_array)

上面的程式碼中還做了在找到當前值的正確位置後跳出內層迴圈。這是因為當找到當前值的正確位置後，就沒有必要繼續比較其他值了。

插入排序時間複雜度

有關時間複雜度的一般性解釋，請訪問此頁面。

有關插入排序時間複雜度的更全面、詳細的解釋，請訪問 此頁面。

選擇排序對 \(n\) 個值的陣列進行排序。

平均而言，每個值必須與大約 \(\frac{n}{2}\) 個其他值進行比較，才能確定將其插入到何處。

並且選擇排序的迴圈必須大約執行 \(n\) 次才能將值插入到其正確的位置。

我們得到插入排序的時間複雜度

\[ O( \frac{n}{2} \cdot n) = \underline{\underline{O(n^2)}} \]

插入排序的時間複雜度可以顯示如下

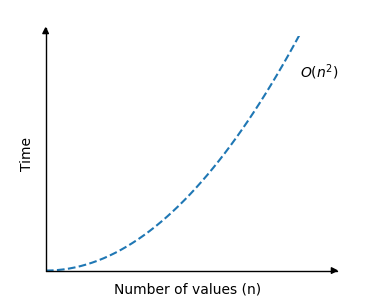
使用下面的模擬來檢視理論時間複雜度 \(O(n^2)\)（紅線）與實際插入排序操作次數的比較。

對於插入排序，最佳、平均和最壞情況場景之間存在很大差異。您可以透過執行上面的不同模擬來檢視。

接下來是快速排序。我們終於將看到一個更快的排序演算法了！