DSA 基數排序

基數排序

基數排序演算法透過對陣列中的每個數字進行排序來完成，從最低有效位（最右邊的位）開始。

基數（或底數）是數字系統中唯一數字的數量。在我們通常使用的十進位制系統中，從 0 到 9 有 10 個不同的數字。

基數排序使用基數，將十進位制值放入 10 個不同的桶（或容器）中，這些桶與當前關注的數字相對應，然後在移動到下一個數字之前，再將它們放回陣列中。

基數排序是一種非比較演算法，僅適用於非負整數。

基數排序演算法可以描述如下：

穩定排序

基數排序必須以穩定方式對元素進行排序，結果才能正確排序。

穩定的排序演算法是一種在排序前後保持相同值元素順序的演算法。假設我們有兩個元素 "K" 和 "L"，其中 "K" 排在 "L" 前面，它們的值都為 "3"。如果元素 "K" 在陣列排序後仍然排在 "L" 前面，則該排序演算法被認為是穩定的。

對於我們之前單獨研究過的演算法，討論穩定排序演算法意義不大，因為無論它們是否穩定，結果都是相同的。但對於基數排序來說，確保在每個數字位置上進行穩定排序非常重要，因為元素一次只按一個數字進行排序。

因此，在對最低有效位上的元素進行排序並移動到下一個數字時，重要的是不要破壞之前數字位置上已完成的排序工作，這就是為什麼我們需要確保基數排序以穩定方式對每個數字位置進行排序。

在下面的模擬中，我們將揭示如何進行底層排序到桶中。為了更好地理解穩定排序的工作原理，您還可以選擇以不穩定方式排序，這將導致不正確的結果。透過簡單地從陣列的末尾而不是開頭將元素放入桶中，可以使排序不穩定。

手動演練

讓我們手動嘗試排序，以便在用程式語言實現基數排序之前，更好地理解它的工作原理。

步驟 1：我們從一個未排序的陣列開始，以及一個空的陣列來容納具有相應基數 0 到 9 的值。

步驟 2：我們開始按關注的最低有效位進行排序。

步驟 3：現在，我們將元素根據關注的數字移動到基數陣列中的正確位置。元素從 myArray 的開頭獲取，並推送到 radixArray 的正確位置。

步驟 4：我們將元素移回初始陣列，現在對最低有效位進行了排序。元素從 radixArray 的末尾獲取，並放入 myArray 的開頭。

步驟 5：我們轉移焦點到下一個數字。請注意，值 45 和 25 仍然保持它們開始時的相對順序，因為我們以穩定方式排序。

步驟 6：根據關注的數字，我們將元素移入基數陣列。

步驟 7：我們將元素從 radixArray 的末尾移回 myArray 的開頭。

排序完成！

執行下面的模擬，以動畫形式檢視以上步驟。

手動執行：發生了什麼？

我們看到值從陣列移出，並根據當前關注的基數放入基數陣列中。然後，這些值又被移回我們要排序的陣列中。

這種從要排序的陣列中移出值然後又移回的操作，必須執行的次數等於值中最大數字的數量。例如，如果陣列中需要排序的最高數字是 437，那麼我們知道必須排序三次，一次處理一個數字。

我們還看到，基數陣列需要是二維的，以便可以容納具有特定基數或索引的多個值。

而且，如前所述，我們必須以一種保持具有相同關注基數的值的順序的方式在兩個陣列之間移動值，這樣排序才是穩定的。

基數排序實現

為了實現基數排序演算法，我們需要：

1. 一個需要排序的非負整數陣列。
2. 一個索引從 0 到 9 的二維陣列，用於儲存當前關注基數的值。
3. 一個迴圈，將值從未排序的陣列中取出，並將其放置在二維基數陣列的正確位置。
4. 一個迴圈，將值從基數陣列移回初始陣列。
5. 一個外迴圈，其執行次數等於最高值中的數字數量。

生成的程式碼如下：

myArray = [170, 45, 75, 90, 802, 24, 2, 66]
print("Original array:", myArray)
radixArray = [[], [], [], [], [], [], [], [], [], []]
maxVal = max(myArray)
exp = 1

while maxVal // exp > 0:

    while len(myArray) > 0:
        val = myArray.pop()
        radixIndex = (val // exp) % 10
        radixArray[radixIndex].append(val)

    for bucket in radixArray:
        while len(bucket) > 0:
            val = bucket.pop()
            myArray.append(val)

    exp *= 10

print("Sorted array:", myArray)

在第 7 行，我們使用地板除法（"//"）將最大值 802 除以 1，這是 while 迴圈第一次執行時。下一次除以 10，最後一次除以 100。使用地板除法（"//"）時，將忽略小數點後的任何數字，並返回一個整數。

在第 11 行，根據值的基數（關注的數字）決定將其放置在 radixArray 中的哪個位置。例如，外層 while 迴圈第二次執行時，exp 將是 10。值 170 除以 10 將得到 17。"%10" 操作將 17 除以 10 一次，餘數為 7。所以值 170 被放入 radixArray 的索引 7。

使用其他排序演算法的基數排序

基數排序實際上可以與任何其他排序演算法一起實現，只要該演算法是穩定的。這意味著，當涉及到按特定數字排序時，任何穩定的排序演算法都可以工作，例如計數排序或氣泡排序。

這是使用氣泡排序對單個數字進行排序的基數排序實現。

def bubbleSort(arr):
    n = len(arr)
    for i in range(n):
        for j in range(0, n - i - 1):
            if arr[j] > arr[j + 1]:
                arr[j], arr[j + 1] = arr[j + 1], arr[j]
                
def radixSortWithBubbleSort(arr):
    max_val = max(arr)
    exp = 1
    
    while max_val // exp > 0:
        radixArray = [[],[],[],[],[],[],[],[],[],[]]
        
        for num in arr:
            radixIndex = (num // exp) % 10
            radixArray[radixIndex].append(num)
        
        for bucket in radixArray:
            bubbleSort(bucket)
        
        i = 0
        for bucket in radixArray:
            for num in bucket:
                arr[i] = num
                i += 1
        
        exp *= 10

myArray = [170, 45, 75, 90, 802, 24, 2, 66]
print("Original array:", myArray)
radixSortWithBubbleSort(myArray)
print("Sorted array:", myArray)

基數排序時間複雜度

有關時間複雜度的一般性解釋，請訪問此頁面。

有關基數排序時間複雜度的更全面和詳細的解釋，請訪問 此頁面。

基數排序的時間複雜度是

\[ \underline{\underline{O(n \cdot k)}} \]

這意味著基數排序既取決於需要排序的值的數量 \(n\)，也取決於最高值 \(k\) 中的數字數量。

基數排序的最佳情況是，如果要排序的值很多，但這些值只有很少的數字。例如，如果要排序的值超過一百萬，而最高值是 999，只有三個數字。在這種情況下，時間複雜度 \(O(n \cdot k)\) 可以簡化為 \(O(n)\)。

基數排序的最壞情況是，最高值中的數字數量與要排序的值的數量相同。這可能不是一種常見情況，但這種情況下時間複雜度將是 \(O(n^2)\)。

最平均或最常見的情況可能是，數字的數量 \(k\) 類似於 \(k(n)= \log n\)。如果是這樣，基數排序的時間複雜度將是 \(O(n \cdot \log n )\)。這種情況的一個例子是，如果要排序 1000000 個值，而這些值有 6 位數字。

請參見下圖所示的基數排序的不同可能時間複雜度。

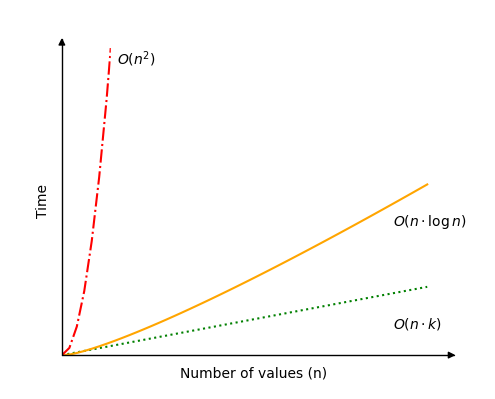
執行基數排序的不同模擬，以檢視操作次數在最壞情況 \(O(n^2)\)（紅線）和最佳情況 \(O(n)\)（綠線）之間如何變化。

代表不同值的條形被縮放到適合視窗，使其看起來還可以。這意味著具有 7 位數字的值看起來只比具有 2 位數字的值大 5 倍，但實際上，具有 7 位數字的值實際上比具有 2 位數字的值大 5000 倍！

如果我們保持 \(n\) 和 \(k\) 固定，模擬中的“隨機”、“降序”和“升序”選項會產生相同數量的操作。這是因為這三種情況都會發生相同的事情。

Radix Sort must use a  
sorting algorithm.