DSA 插入排序時間複雜度

有關時間複雜度的通用解釋，請參閱此頁面。

插入排序時間複雜度

插入排序最壞情況的場景是陣列已經排序，但數值是從大到小排列的。這是因為在這種情況下，每個新值都必須“穿過”整個已排序的陣列部分。

以下是插入排序演算法為前幾個元素執行的操作：

• 第 1 個值已在正確的位置。
• 第 2 個值必須與第 1 個值進行比較並移到其後。
• 第 3 個值必須與前面兩個值進行比較並移到它們之後。
• 第 3 個值必須與前面三個值進行比較並移到它們之後。
• 以此類推……

如果我們繼續這種模式，那麼對於 \(n\) 個值，總操作次數為：

\[1+2+3+...+(n-1)\]

這是數學中一個眾所周知的數列，可以寫成：

\[ \frac{n(n-1)}{2} = \frac{n^2}{2} - \frac{n}{2} \]

對於非常大的 \(n\)，\(\frac{n^2}{2}\) 項占主導地位，因此我們可以透過移除第二項 \(\frac{n}{2}\) 來簡化。

使用大 O 符號，插入排序演算法的時間複雜度為：

\[ O(\frac{n^2}{2}) = O(\frac{1}{2} \cdot n^2) = \underline{\underline{O(n^2)}} \]

時間複雜度可以顯示如下：

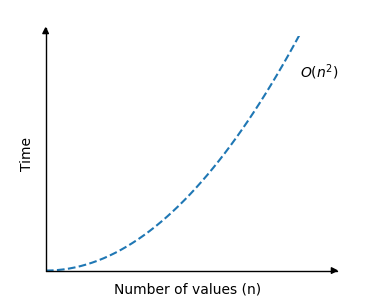
如您所見，當值 \(n\) 增加時，插入排序使用的時間會快速增加。

插入排序模擬

使用下面的模擬來檢視理論時間複雜度 \(O(n^2)\)（紅線）與實際插入排序操作次數的比較。

對於插入排序，最佳、平均和最壞情況場景之間存在很大差異。您可以透過執行上面的不同模擬來檢視。

上面的紅線代表理論上的上限時間複雜度 \(O(n^2)\)，而實際函式是 \(1.07 \cdot n^2\)。

請記住，如果存在一個正常量 \(C\) 使得 \(C \cdot g(n)>f(n)\)，則稱函式 \(f(n)\) 為 \(O(g(n))\)。

在這種情況下，\(f(n)\) 是插入排序使用的運算元，\(g(n)=n^2\)，而 \(C=1.07\)。