DSA 合併排序

合併排序

合併排序演算法是一種分治演算法，它透過先將陣列分解成更小的陣列，然後以正確的方式將陣列重新組合起來，使其有序。

分解：演算法從將陣列分解成越來越小的部分開始，直到一個子陣列只包含一個元素。

合併：演算法透過將最低值放在前面，將陣列的小部分重新合併在一起，從而得到一個排序後的陣列。

分解和構建陣列以對其進行排序是透過遞迴完成的。

在上面的動畫中，每次條形圖被推下去都代表一次遞迴呼叫，將陣列分成更小的部分。當條形圖被抬起時，表示兩個子陣列已被合併在一起。

合併排序演算法可以這樣描述：

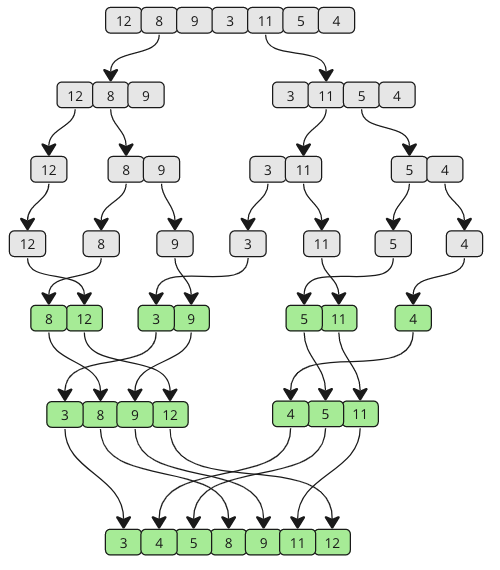
從不同的角度看看下面的圖，瞭解合併排序的工作原理。正如你所見，陣列被分解成越來越小的部分，直到重新合併。在合併過程中，會比較每個子陣列中的值，以便最低的值排在前面。

手動演練

在實際用程式語言實現之前，讓我們手動嘗試排序，以便更好地理解合併排序的工作原理。

步驟 1：我們從一個未排序的陣列開始，並且我們知道它會被分成兩半，直到子陣列只包含一個元素。Merge Sort 函式呼叫自身兩次，一次用於陣列的每個一半。這意味著第一個子陣列將首先分解成最小的部分。

步驟 2：第一個子陣列的分解完成，現在是合併的時候了。8 和 9 是要合併的前兩個元素。8 是最小值，所以它排在第一個合併的子陣列的 9 前面。

步驟 3：要合併的下一個子陣列是 [ 12] 和 [ 8, 9]。兩個陣列中的值都從開始進行比較。8 小於 12，所以 8 排在前面，9 也小於 12。

步驟 4：現在第二個大的子陣列被遞迴分解。

步驟 5：3 和 11 以它們顯示的相同順序合併在一起，因為 3 小於 11。

步驟 6：包含 5 和 4 的子陣列被分解，然後合併，使 4 排在 5 前面。

步驟 7：右邊的兩個子陣列被合併。進行比較以建立新合併陣列中的元素。

1. 3 小於 4
2. 4 小於 11
3. 5 小於 11
4. 11 是最後剩餘的值

步驟 8：最後剩餘的兩個子陣列被合併。讓我們更詳細地看看比較是如何進行的，以便建立新的合併的、最終排序的陣列。

3 小於 8

步驟 9：4 小於 8

步驟 10：5 小於 8

步驟 11：8 和 9 小於 11

步驟 12：11 小於 12

排序完成！

執行下面的模擬，以動畫形式檢視以上步驟。

{{ x.dieNmbr }}

手動執行：發生了什麼？

我們看到該演算法有兩個階段：首先是分解，然後是合併。

雖然可以在不使用遞迴的情況下實現合併排序演算法，但我們將使用遞迴，因為這是最常見的方法。

在上面的步驟中我們看不到，但為了將陣列分成兩半，陣列的長度除以二，然後向下取整得到一個稱為“mid”的值。這個“mid”值用作分割陣列的索引。

在陣列被分割後，排序函式會用每個子陣列呼叫自身，以便陣列可以遞迴地再次分割。分割會一直持續到子陣列只包含一個元素。

在 Merge Sort 函式的末尾，子陣列被合併，因此在陣列重新構建時，子陣列始終是有序的。為了合併兩個子陣列並使其結果有序，會將每個子陣列的值進行比較，並將最低值放入合併的陣列中。之後，將比較兩個子陣列中的下一個值，將較低的值放入合併的陣列中。

合併排序實現

要實現合併排序演算法，我們需要：

1. 一個包含需要排序的值的陣列。
2. 一個函式，它接受一個數組，將其分成兩半，並用該陣列的每個一半呼叫自身，以便陣列一遍又一遍地遞迴分割，直到子陣列只包含一個值。
3. 另一個函式，它以排序的方式將子數組合並回在一起。

生成的程式碼如下：

def mergeSort(arr):
    if len(arr) <= 1:
        return arr

    mid = len(arr) // 2
    leftHalf = arr[:mid]
    rightHalf = arr[mid:]

    sortedLeft = mergeSort(leftHalf)
    sortedRight = mergeSort(rightHalf)

    return merge(sortedLeft, sortedRight)

def merge(left, right):
    result = []
    i = j = 0

    while i < len(left) and j < len(right):
        if left[i] < right[j]:
            result.append(left[i])
            i += 1
        else:
            result.append(right[j])
            j += 1

    result.extend(left[i:])
    result.extend(right[j:])

    return result

unsortedArr = [3, 7, 6, -10, 15, 23.5, 55, -13]
sortedArr = mergeSort(unsortedArr)
print("Sorted array:", sortedArr)

在第 6 行，arr[:mid] 獲取陣列中直到索引“mid”之前的所有值（不包括該值）。

在第 7 行，arr[mid:] 獲取陣列中從索引“mid”開始的所有值以及之後的所有值。

在第 26-27 行，完成合並的第一部分。此時比較兩個子陣列的值，並且左子陣列或右子陣列為空，因此結果陣列可以只用左子陣列或右子陣列的剩餘值填充。這些行可以互換，結果將相同。

不使用遞迴的合併排序

由於合併排序是一種分治演算法，因此遞迴是實現中最直觀的程式碼。合併排序的遞迴實現也可能更容易理解，並且通常程式碼行數更少。

但是，合併排序也可以在不使用遞迴的情況下實現，這樣函式就不會呼叫自身。

看看下面不使用遞迴的合併排序實現。

def merge(left, right):
    result = []
    i = j = 0
    
    while i < len(left) and j < len(right):
        if left[i] < right[j]:
            result.append(left[i])
            i += 1
        else:
            result.append(right[j])
            j += 1
            
    result.extend(left[i:])
    result.extend(right[j:])
    
    return result

def mergeSort(arr):
    step = 1  # Starting with sub-arrays of length 1
    length = len(arr)
    
    while step < length:
        for i in range(0, length, 2 * step):
            left = arr[i:i + step]
            right = arr[i + step:i + 2 * step]
            
            merged = merge(left, right)
            
            # Place the merged array back into the original array
            for j, val in enumerate(merged):
                arr[i + j] = val
                
        step *= 2  # Double the sub-array length for the next iteration
        
    return arr

unsortedArr = [3, 7, 6, -10, 15, 23.5, 55, -13]
sortedArr = mergeSort(unsortedArr)
print("Sorted array:", sortedArr)

您可能會注意到，上面兩個合併排序實現中的合併函式是完全相同的，但在上面的實現中，mergeSort 函式內的 while 迴圈用於替換遞迴。while 迴圈以原地方式完成陣列的分割和合並，這使得程式碼有點難以理解。

簡單來說，mergeSort 函式內的 while 迴圈使用較短的步長，使用 merge 函式對初始陣列的微小部分（子陣列）進行排序。然後增加步長以合併和排序陣列的更大部分，直到整個陣列被排序。

合併排序時間複雜度

有關時間複雜度的一般性解釋，請訪問此頁面。

有關合並排序時間複雜度的更全面和詳細的解釋，請訪問此頁面。

合併排序的時間複雜度為：

\[ O( n \cdot \log n ) \]

對於不同種類的陣列，時間複雜度幾乎相同。無論陣列是已排序還是完全打亂，演算法都需要分割陣列並將其合併回在一起。

下圖顯示了合併排序的時間複雜度。

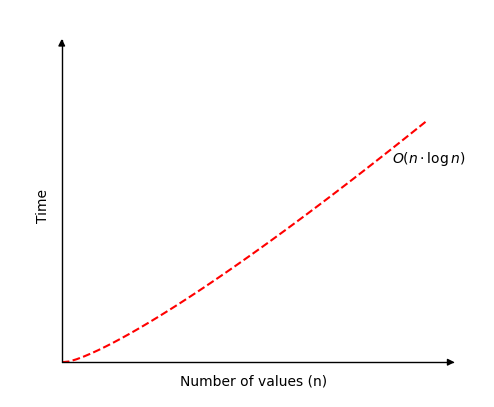
執行下面的模擬，對陣列中的不同數量的值進行操作，並檢視合併排序對 n 個元素的陣列所需的次數是 O(n log n)。

如果我們固定值的數量 n，則“隨機”、“降序”和“升序”所需的操作次數幾乎相同。

合併排序每次的表現幾乎相同，因為陣列是根據比較進行分割和合並的，無論陣列是否已排序。