DSA 合併排序時間複雜度

有關時間複雜度的通用解釋，請參閱此頁面。

合併排序時間複雜度

Merge Sort 演算法將陣列分解成越來越小的片段。

當子陣列被合併回一起，並且最小的值排在前面時，陣列就會被排序。

需要排序的陣列有 \(n\) 個值，我們可以透過檢視演算法所需的 the number of operations 來找到時間複雜度。

Merge Sort 主要的操作是分割，然後透過比較元素來進行合併。

為了將陣列從頭開始分割，直到子陣列只包含一個值，Merge Sort 總共需要 \(n-1\) 次分割。想象一個包含 16 個值的陣列。它被分割一次成長度為 8 的子陣列，再次分割，再分割，子陣列的大小減小到 4、2，最後是 1。對於一個 16 個元素的陣列，分割次數是 \(1+2+4+8=15\)。

下圖顯示了對包含 16 個數字的陣列需要 15 次分割。

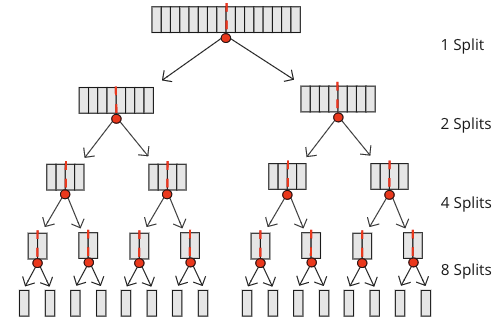
合併的次數實際上也是 \(n-1\) 次，與分割次數相同，因為每次分割都需要一次合併來重建陣列。每次合併時，都會對子陣列中的值進行比較，以便合併結果是有序的。

在合併兩個子陣列時，生成最多比較的 worst case scenario 是子陣列大小相等。考慮合併 [1,4,6,9] 和 [2,3,7,8]。在這種情況下，需要進行以下比較：

1. 比較 1 和 2，結果：[1]
2. 比較 4 和 2，結果：[1,2]
3. 比較 4 和 3，結果：[1,2,3]
4. 比較 4 和 7，結果：[1,2,3,4]
5. 比較 6 和 7，結果：[1,2,3,4,6]
6. 比較 9 和 7，結果：[1,2,3,4,6,7]
7. 比較 9 和 8，結果：[1,2,3,4,6,7,8]

在合併結束時，只有一個數組中還剩下值 9，另一個數組為空，因此不需要比較就可以將最後一個值放入，合併後的陣列是 [1,2,3,4,6,7,8,9]。我們看到合併 8 個值（每個初始子陣列 4 個值）需要 7 次比較。總的來說，在 worst case scenario 中，合併 \(n\) 個值需要 \(n-1\) 次比較。

為了簡化，我們假設合併 \(n\) 個值需要 \(n\) 次比較而不是 \(n-1\) 次。當 \(n\) 很大時，這可以接受，因為我們想使用 Big O 符號計算一個上限。

因此，在每個合併發生的層級，需要 \(n\) 次比較，有多少層呢？好吧，對於 \(n=16\)，我們有 \(n=16=2^4\)，所以有 4 層合併。對於 \(n=32=2^5\)，有 5 層合併，每層需要 \(n\) 次比較。對於 \(n=1024=2^{10}\)，需要 10 層合併。要找出 2 的多少次方等於 1024，我們使用以 2 為底的對數。答案是 10。數學上看起來是這樣的：\( \log_{2}1024=10\)。

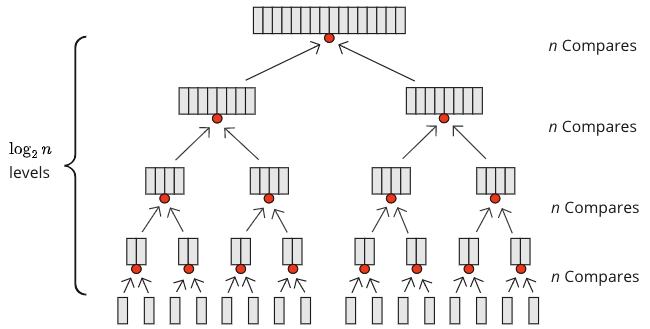
正如我們在上面的圖表中看到的，每層需要 \(n\) 次比較，並且有 \( \log_{2}n\) 層，所以總共有 \( n \cdot \log_{2}n\) 次比較操作。

時間複雜度可以根據分割操作次數和合並操作次數來計算。

\[ \begin{equation} \begin{aligned} O( (n-1) + n \cdot \log_{2}n) {} & = O( n \cdot \log_{2}n ) \end{aligned} \end{equation} \]

分割操作次數 \((n-1)\) 可以從上面的 Big O 計算中移除，因為對於大的 \(n\)，\( n \cdot \log_{2}n\) 將佔主導地位，並且這是我們計算演算法時間複雜度的方式。

下圖顯示了當 Merge Sort 在一個具有 \(n\) 個值的陣列上執行時，時間是如何增加的。

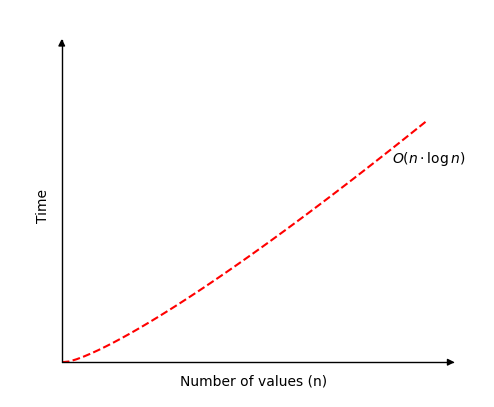
與其他許多排序演算法相比，Merge Sort 的最好和最壞情況之間的差異並不大。

Merge Sort 模擬

執行模擬，嘗試不同的陣列值數量，看看 Merge Sort 在一個包含 \(n\) 個元素的陣列上需要的操作次數 \(O(n \log n)\)

如果我們將值的數量 \(n\) 固定，"隨機"、"降序"和"升序"所需的運算元量幾乎相同。

Merge Sort 每次執行的效能幾乎相同，因為陣列被分割和合並（使用比較），無論陣列是否已排序。