DSA 選擇排序時間複雜度

有關時間複雜度的通用解釋，請參閱此頁面。

選擇排序時間複雜度

選擇排序演算法 遍歷陣列中的所有元素，找到最小值，並將其移動到陣列的開頭，然後一遍又一遍地重複此操作，直到陣列排序完成。

選擇排序會遍歷一個包含 \(n\) 個值的陣列 \(n-1\) 次。這是因為當演算法只剩下最後一個值未排序時，最後一個值也必然已在其正確的位置。

演算法第一次遍歷陣列時，會比較所有值以找出哪個是最小的。

演算法第二次遍歷陣列時，會比較除第一個值之外的所有值以找出哪個是最小的。

就這樣，陣列中未排序的部分越來越短，直到排序完成。因此，平均而言，當演算法遍歷陣列以查詢最小值並將其移動到陣列開頭時，會考慮 \(\frac{n}{2}\) 個元素。

除了所有需要的比較之外，需要的交換次數為 \(n \)。

我們可以開始計算選擇排序演算法的操作次數

\[ \begin{equation} \begin{aligned} 操作次數 {} & = (n-1)\cdot \frac{n}{2} + n \\ & = \frac{n^2}{2} - \frac{n}{2} + n \\ & = \frac{n^2}{2} + \frac{n}{2} \end{aligned} \end{equation} \]

在考慮演算法的執行時間時，我們關注非常大的資料集，這意味著 \(n\) 是一個非常大的數字。對於非常大的數字 \(n\)，\(\frac{n^2}{2}\) 項比 \(\frac{n}{2}\) 項大得多，我們可以透過簡單地去掉第二項 \(\frac{n}{2}\) 來近似。

\[操作次數 = \frac{n^2}{2} + \frac{n}{2} \approx \frac{n^2}{2} = \frac{1}{2} \cdot n^2 \]

使用大 O 表示法來描述選擇排序演算法的時間複雜度，我們得到

\[ O( \frac{1}{2} \cdot n^2) = \underline{\underline{O(n^2)}} \]

選擇排序演算法的時間複雜度可以用這樣的圖表顯示

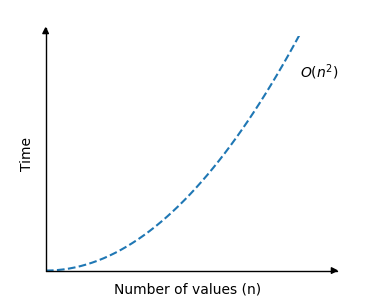
正如您所見，執行時間與氣泡排序相同：當增加陣列大小時，執行時間會迅速增加。

選擇排序模擬

執行不同數量值的陣列的模擬，並檢視選擇排序在 \(n\) 個元素的陣列上所需的操作次數為 \(O(n^2)\)

與氣泡排序相比，我們在此模擬中注意到的最顯著的區別是，選擇排序的最佳和最壞情況實際上幾乎相同 (\(O(n^2)\))，但對於氣泡排序，最佳情況執行時間僅為 \(O(n)\)。

選擇排序在最佳和最壞情況下的主要區別在於交換次數。在最佳情況下，選擇排序無需交換任何值，因為陣列已排序。而在最壞情況下，陣列已排序但順序錯誤，因此選擇排序必須進行與陣列中值數量相同的交換。