DSA 快速排序

快速排序

顧名思義，快速排序是最快的排序演算法之一。

快速排序演算法接受一個值陣列，選擇其中一個值作為“樞軸”元素，然後移動其他值，使得較小的值位於樞軸元素的左側，較大的值位於其右側。

在本教程中，我們選擇陣列的最後一個元素作為樞軸元素，但我們也可以選擇陣列的第一個元素，或者實際上是陣列中的任何元素。

然後，快速排序演算法遞迴地對樞軸元素左右兩側的子陣列執行相同的操作。這會一直持續到陣列被排序。

該演算法可以描述為：

請繼續閱讀，以全面瞭解快速排序演算法以及如何自己實現它。

手動演練

在我們用程式語言實現快速排序演算法之前，讓我們手動地遍歷一個簡短的陣列，以便了解其原理。

步驟 1：我們從一個未排序的陣列開始。

步驟 2：我們選擇最後一個值 3 作為樞軸元素。

步驟 3：陣列中的其餘值都大於 3，並且必須在 3 的右側。將 3 和 11 交換。

步驟 4：值 3 現在處於正確的位置。我們需要對 3 右側的值進行排序。我們選擇最後一個值 11 作為新的樞軸元素。

步驟 5：值 7 必須位於樞軸值 11 的左側，而 12 必須位於其右側。移動 7 和 12。

步驟 6：將 11 和 12 交換，以便較小的值 9 和 7 位於 11 的左側，而 12 位於右側。

步驟 7：11 和 12 處於正確的位置。我們選擇 7 作為子陣列 [ 9, 7] 中 11 左側的樞軸元素。

步驟 8：我們必須交換 9 和 7。

現在，陣列已排序。

執行下面的模擬，以動畫形式檢視以上步驟。

手動執行：發生了什麼？

在我們用程式語言實現演算法之前，需要更詳細地回顧一下上面發生的事情。

我們已經知道陣列的最後一個值被選為樞軸元素，而其餘值被排列成小於樞軸值的值在左側，大於樞軸值的值在右側。

之後，樞軸元素與較高值中的第一個元素交換。這會將原始陣列分成兩部分，樞軸元素位於較低值和較高值之間。

現在，我們需要對舊樞軸元素左右兩側的子陣列執行相同的操作。如果子陣列的長度為 0 或 1，我們則認為它已排序。

總而言之，快速排序演算法使子陣列越來越短，直到陣列被排序。

快速排序實現

為了編寫一個 'quickSort' 方法來將陣列分割成越來越短的子陣列，我們使用遞迴。這意味著 'quickSort' 方法必須用樞軸元素左右兩側的新子陣列來呼叫自身。在此處閱讀有關遞迴的更多資訊：此處。

要在程式語言中實現快速排序演算法，我們需要：

1. 一個包含待排序值的陣列。
2. 一個 quickSort 方法，如果子陣列的大小大於 1，它會呼叫自身（遞迴）。
3. 一個 partition 方法，它接收一個子陣列，移動值，將樞軸元素交換到子陣列中，並返回下一個子陣列分割發生的位置索引。

生成的程式碼如下：

def partition(array, low, high):
    pivot = array[high]
    i = low - 1

    for j in range(low, high):
        if array[j] <= pivot:
            i += 1
            array[i], array[j] = array[j], array[i]

    array[i+1], array[high] = array[high], array[i+1]
    return i+1

def quicksort(array, low=0, high=None):
    if high is None:
        high = len(array) - 1

    if low < high:
        pivot_index = partition(array, low, high)
        quicksort(array, low, pivot_index-1)
        quicksort(array, pivot_index+1, high)

my_array = [64, 34, 25, 12, 22, 11, 90, 5]
quicksort(my_array)
print("Sorted array:", my_array)

快速排序時間複雜度

有關時間複雜度的一般性解釋，請訪問此頁面。

有關快速排序時間複雜度的更全面、詳細的解釋，請訪問此頁面。

快速排序的最壞情況是 \(O(n^2) \)。這是因為樞軸元素是每個子陣列中的最高值或最低值，這會導致大量遞迴呼叫。使用我們上面的實現，當陣列已經排序時就會發生這種情況。

但平均而言，快速排序的時間複雜度實際上只有 \(O(n \log n) \)，這比我們之前看過的排序演算法要好得多。這就是快速排序如此受歡迎的原因。

在下面的模擬中，您可以看到快速排序在平均場景 \(O(n \log n) \) 下的時間複雜度與之前排序演算法（氣泡排序、選擇排序和插入排序）的時間複雜度 \(O(n^2) \) 相比有了顯著的提高。

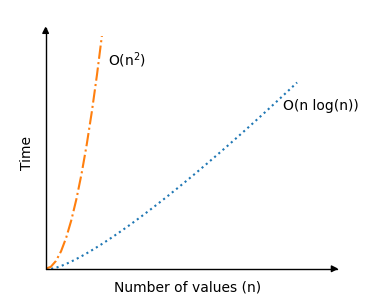
快速排序演算法的遞迴部分實際上是平均排序場景之所以如此快速的原因，因為如果樞軸元素選擇得當，陣列每次呼叫演算法時都會大致平均地分成兩半。因此，即使值的數量 \(n \) 加倍，遞迴呼叫的次數也不會加倍。

在下面的模擬中，使用不同數量的值和不同型別的陣列執行快速排序。

def partition(array, low, high):
    pivot = array[high]
    i = low - 1

    for j in range(low, high):
        if array[j] <= pivot:
            i += 1
            array[i], array[j] = array[j], array[i]

    array[i+1], array[high] = array[high], array[i+1]
    return i+1

def quicksort(array, low=0, high=None):
    if high is None:
        high = len(array) - 1

    if low < high:
        pivot_index = partition(array, low, high)
        (array, low, pivot_index-1)
        (array, pivot_index+1, high)

my_array = [64, 34, 25, 12, 22, 11, 90, 5]
quicksort(my_array)
print("Sorted array:", my_array)