DSA 計數排序時間複雜度

有關時間複雜度的通用解釋，請參閱此頁面。

計數排序時間複雜度

計數排序的工作原理是首先計算不同值的出現次數，然後利用這些次數來按排序順序重構陣列。

經驗法則是，當可能值的範圍 \(k\) 小於值的數量 \(n\) 時，計數排序演算法的執行速度很快。

要使用大 O 表示法表示時間複雜度，我們首先需要計算演算法執行的運算元。

• 查詢最大值：必須對每個值進行一次評估，以確定它是否為最大值，因此需要 \(n\) 次操作。
• 初始化計數陣列：在陣列中的最大值為 \(k\) 的情況下，我們需要 \(k+1\) 個元素在計數陣列中，以便包含 0。計數陣列中的每個元素都必須初始化，因此需要 \(k+1\) 次操作。
• 我們要排序的每個值都會被計數一次，然後刪除，因此每次計數需要 2 次操作，總共 \(2 \cdot n\) 次操作。
• 構建排序陣列：建立排序陣列中的 \(n\) 個元素：\(n\) 次操作。

總計我們得到

\[ \begin{equation} \begin{aligned} 操作 {} & = n + (k+1) + (2 \cdot n) + n \\ & = 4 \cdot n + k + 1 \\ & \approx 4 \cdot n + k \end{aligned} \end{equation} \]

根據我們之前對時間複雜度的瞭解，我們可以建立一個簡化的表示式，使用大 O 表示法來表示時間複雜度。

\[ \begin{equation} \begin{aligned} O(4 \cdot n + k) {} & = O(4 \cdot n) + O(k) \\ & = O(n) + O(k) \\ & = \underline{\underline{O(n+k)}} \end{aligned} \end{equation} \]

正如前面所提到的，計數排序在不同值的範圍 \(k\) 相對於要排序的值的總數 \(n\) 較小時是有效的。我們現在可以直接從大 O 表示式 \(O(n+k)\) 中看出這一點。

例如，假設不同數字的範圍 \(k\) 是要排序的值的數量的 10 倍。在這種情況下，我們可以看到演算法花費了大部分時間來處理不同數字的範圍 \(k\)，儘管要排序的實際值 \(n\) 相比較小。

對於計數排序，在圖表中顯示時間複雜度或進行時間複雜度模擬並不直接，因為時間複雜度受到值範圍 \(k\) 的很大影響。

下面是一個圖表，顯示了計數排序的時間複雜度可能有多大差異，隨後是對最佳和最壞情況的解釋。

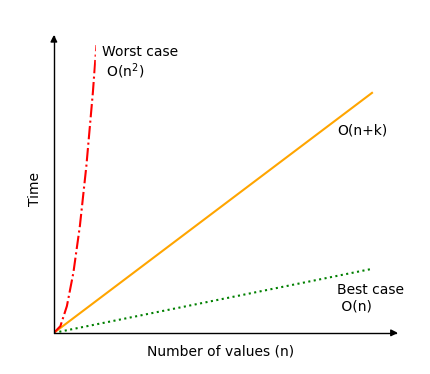
計數排序的最佳情況是範圍 \(k\) 僅佔 \(n\) 的一小部分，例如 \(k(n)=0.1 \cdot n\)。例如，對於 100 個值，範圍是從 0 到 10；或者對於 1000 個值，範圍是從 0 到 100。在這種情況下，我們得到時間複雜度 \(O(n+k)=O(n+0.1 \cdot n) = O(1.1 \cdot n)\)，簡寫為 \(O(n)\)。

然而，最壞情況是範圍遠大於輸入。假設對於僅 10 個值的輸入，範圍在 0 到 100 之間；或者類似地，對於 1000 個值的輸入，範圍在 0 到 1000000 之間。在這種情況下，\(k\) 的增長相對於 \(n\) 是二次的，如下所示：\(k(n)=n^2\)，我們得到時間複雜度 \(O(n+k)=O(n+n^2)\)，簡寫為 \(O(n^2)\)。甚至比這更糟糕的情況也可能出現，但選擇這種情況是因為它相對容易理解，而且也許並不那麼不現實。

正如你所看到的，在選擇計數排序作為你的演算法之前，考慮值的範圍與要排序的值的數量進行比較是很重要的。此外，如頁面頂部所述，請記住計數排序僅適用於非負整數值。

計數排序模擬

執行計數排序的不同模擬，以瞭解操作次數如何在最壞情況 \(O(n^2)\)（紅線）和最佳情況 \(O(n)\)（綠線）之間變化。

如前所述：如果要排序的數字值變化很大（\(k\) 大），而要排序的數字很少（\(n\) 小），則計數排序演算法無效。

如果我們保持 \(n\) 和 \(k\) 固定，模擬中的“隨機”、“降序”和“升序”選項會導致相同數量的操作。這是因為在這三種情況中發生的事情是相同的：設定一個計數陣列，對數字進行計數，然後建立新的排序陣列。