統計 - 正態分佈

正態分佈是統計學中一個重要的機率分佈。

許多現實世界的資料都呈正態分佈。

正態分佈

正態分佈由均值 (\(\mu\)) 和標準差 (\(\sigma\)) 描述。

正態分佈由於其形狀，通常被稱為“鐘形曲線”。

• 大多數值都集中在中心 (\(\mu\)) 附近。
• 中位數和均值相等。
• 它只有一個眾數。
• 它具有對稱性，這意味著它在中心兩側的下降量相同。

正態分佈曲線下的面積代表資料的機率。

整個曲線下的面積等於 1，即 100%。

這是正態分佈在標準差 (\(\sigma\)) 之間的機率圖。

• 大約 68.3% 的資料在平均值（從 μ-1σ 到 μ+1σ）的一個標準差範圍內。
• 大約 95.5% 的資料在平均值的兩個標準差範圍內（從 μ-2σ 到 μ+2σ）。
• 大約 99.7% 的資料在平均值的三個標準差範圍內（從 μ-3σ 到 μ+3σ）。

不同的均值和標準差

均值描述了正態分佈的中心位置。

這是一張顯示三個具有相同標準差但均值不同的正態分佈的圖。

標準差描述了正態分佈的擴散程度。

這是一張顯示三個具有相同均值但標準差不同的正態分佈的圖。

紫色曲線的標準差最大，黑色曲線的標準差最小。

每條曲線下的面積仍然是 1，即 100%。

正態分佈資料的真實資料示例

現實世界的資料通常呈正態分佈。

這是一個諾貝爾獎獲得者獲獎時的年齡直方圖。

繪製在直方圖上方的正態分佈是基於真實資料的總體均值 (\(\mu\)) 和標準差 (\(\sigma\))。

我們可以看到直方圖接近正態分佈。

可能呈正態分佈的現實世界變數的示例

• 考試成績
• 高度
• 出生體重

機率分佈

機率分佈是計算隨機變數結果機率的函式。

隨機變數的典型示例是拋硬幣和擲骰子。

這是一張圖，顯示了拋硬幣次數不斷增加的結果以及預期的結果（正面或反面）。

拋硬幣的預期值是拋硬幣的機率分佈。

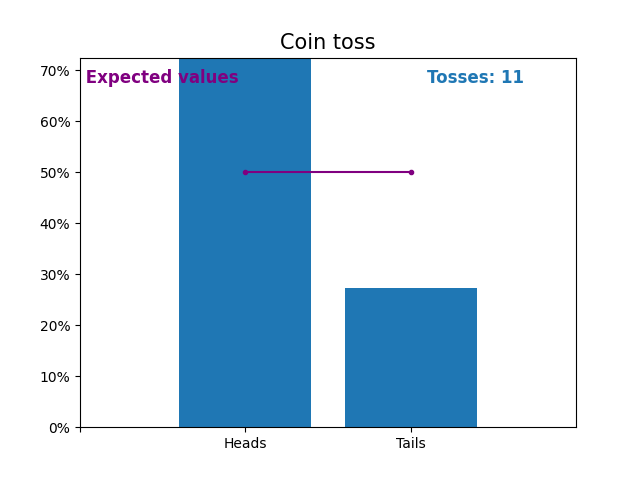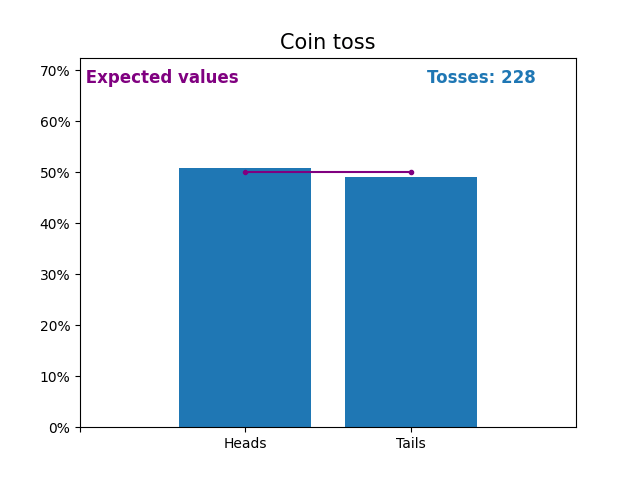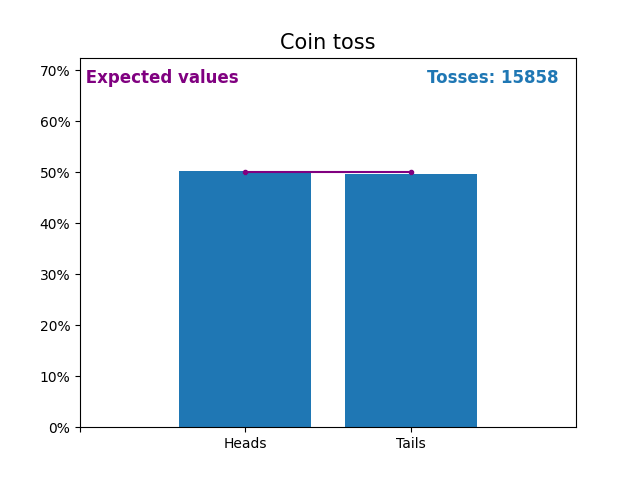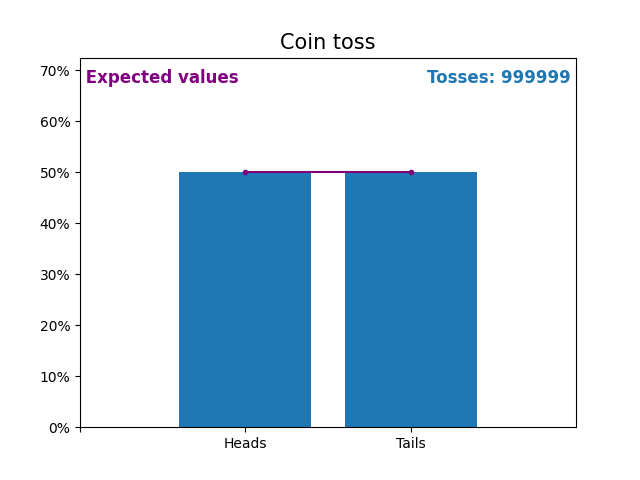
請注意，隨著拋硬幣次數的增加，隨機拋硬幣的結果如何越來越接近預期值（50%）。

同樣，這是一張圖，顯示了擲骰子次數不斷增加的結果以及預期的結果（從 1 到 6）。

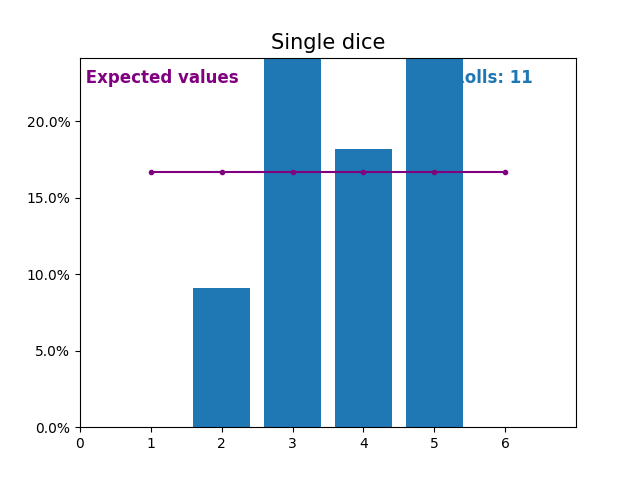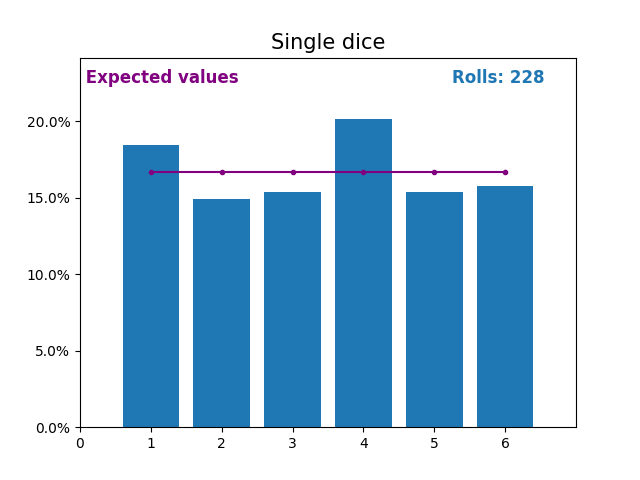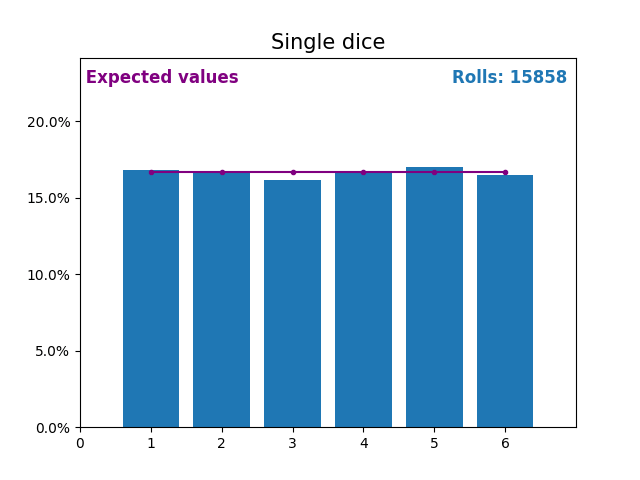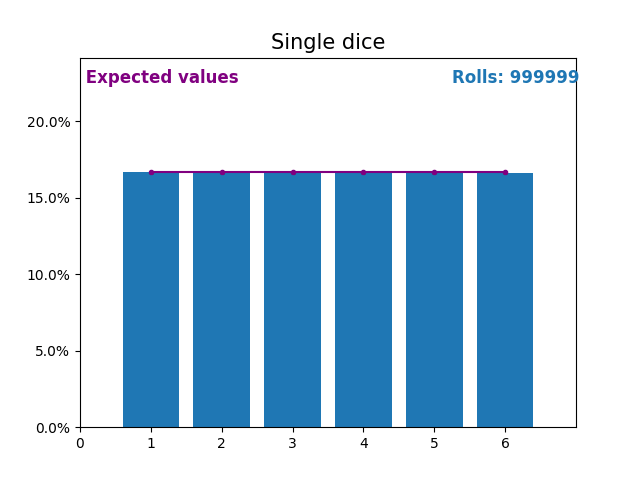
再次注意，隨著擲骰子次數的增加，隨機擲骰子的結果如何越來越接近預期值（1/6，或 16.666%）。

當隨機變數是骰子點數之和時，結果和預期值會呈現不同的形狀。

不同的形狀來自於得到中間值附近的和的方式比得到小或大的和的方式更多。

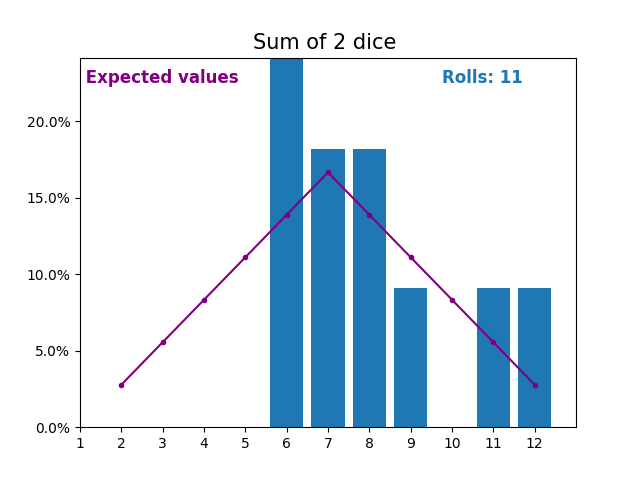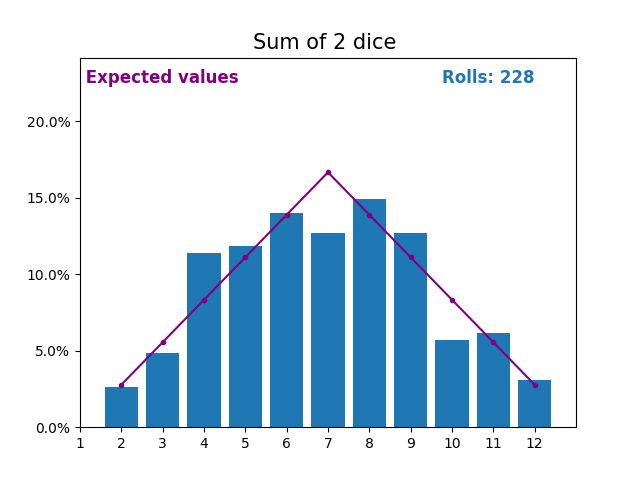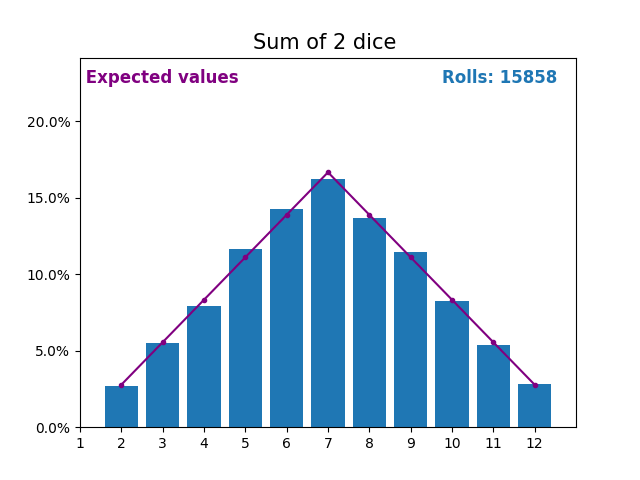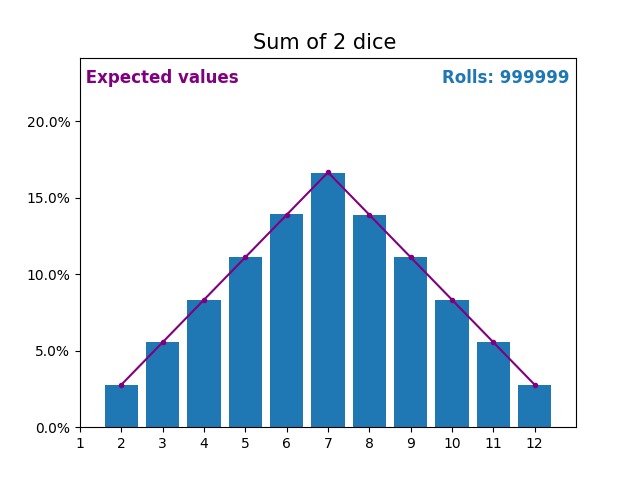
隨著我們不斷增加用於求和的骰子數量，結果和預期值的形狀越來越像正態分佈。

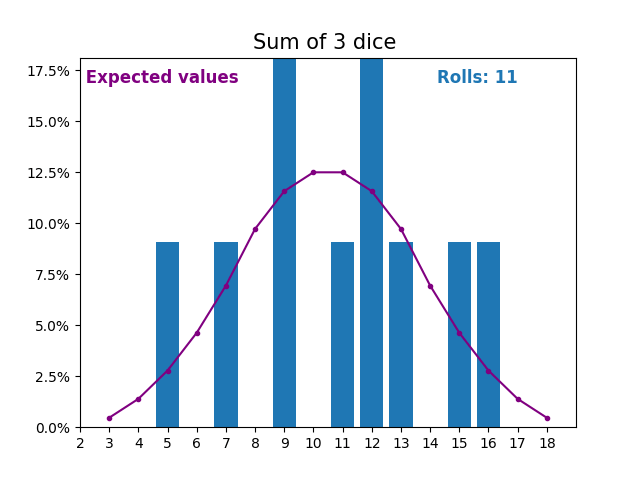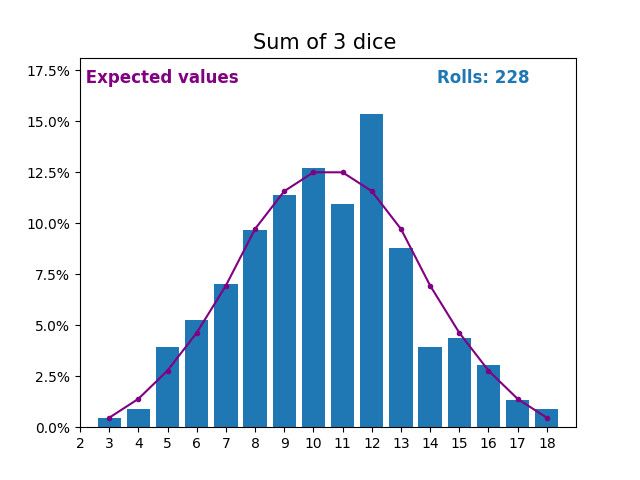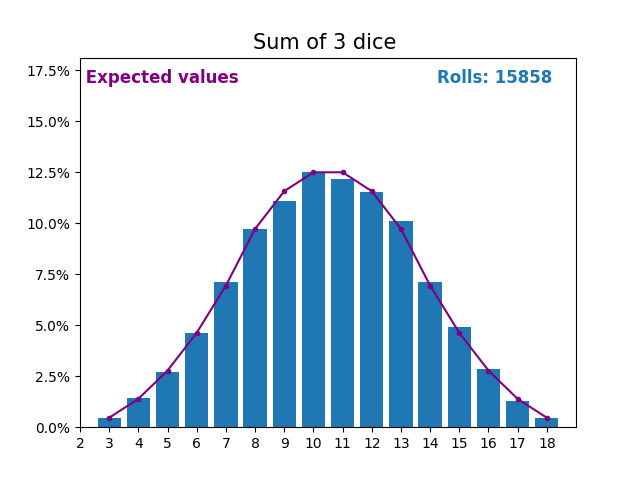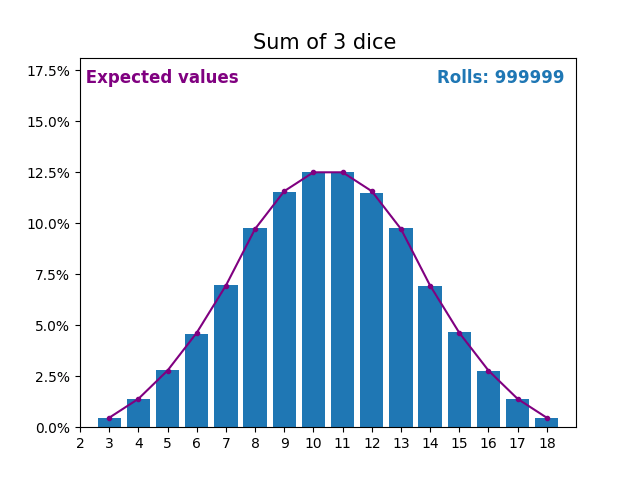
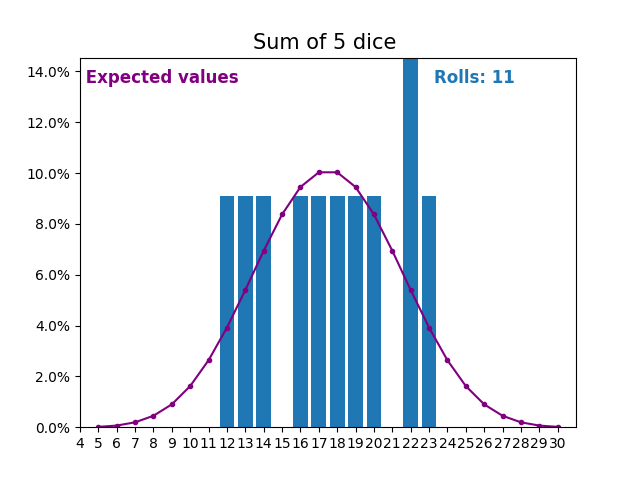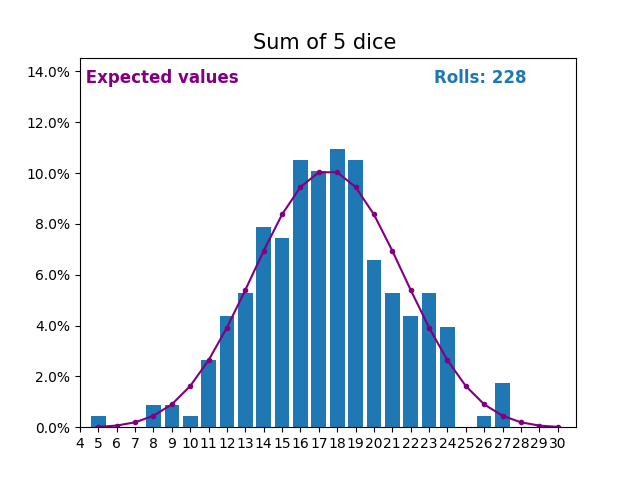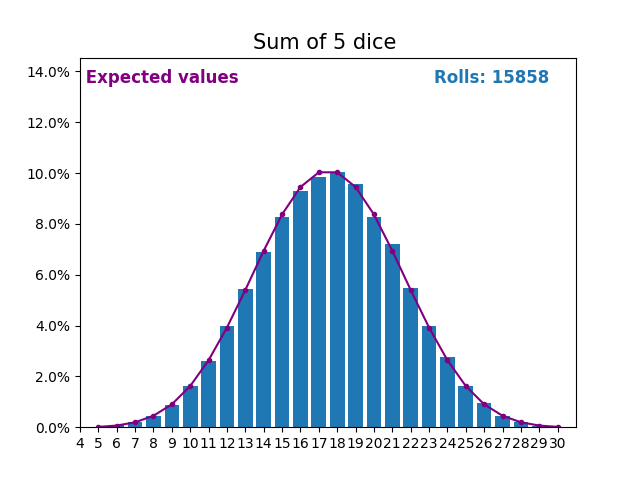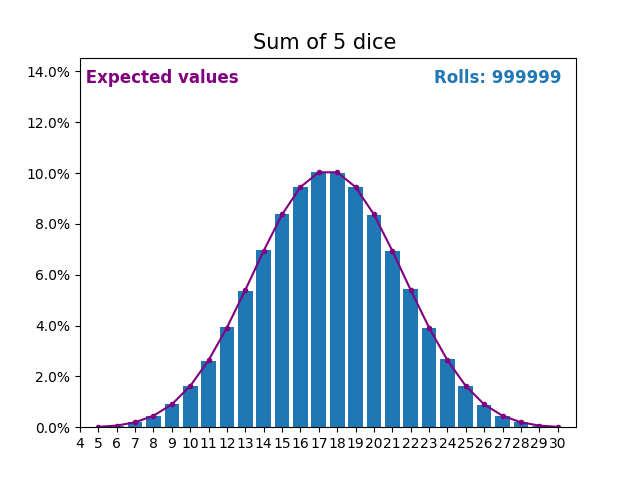
許多現實世界的變數遵循相似的模式，並自然形成正態分佈。

正態分佈變數可以使用眾所周知的技術進行分析。

您將在接下來的幾頁中學習一些最常見和最有用的技術。