向量

向量表示法

向量有多種寫法。最常見的是

或

幾何中的向量

左圖是向量。 長度顯示大小。 箭頭顯示方向。

運動

向量是運動的基本組成部分

在幾何學中，向量可以描述從一個點到另一個點的移動。

向量 [3, 2] 表示向右移動 3 個單位，向上移動 2 個單位。

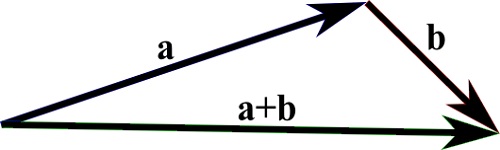
向量加法

兩個向量 (a+b) 的和是透過將向量 b 移動到向量 a 的頭部，使其尾部與向量 a 的頭部相遇而找到的。（這不會改變向量 b）。

然後，從 a 的尾部到 b 的頭部的連線就是向量 a+b

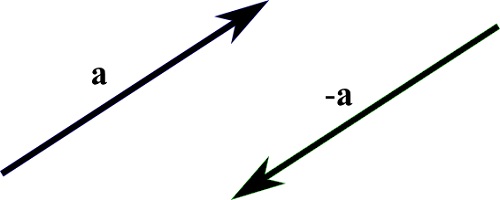
向量減法

向量 -a 是 +a 的相反。

這意味著向量 a 和向量 -a 在相反方向上具有相同的大小

標量運算

向量可以透過將標量（數字）加、減或乘以所有向量值來修改

a = [1 1 1]

a + 1 = [2 2 2]

[1 2 3] + 1 = [2 3 4]

向量乘法與普通乘法具有許多相同的性質

[2 2 2] * 3 = [6 6 6]

[6 6 6] / 3 = [2 2 2]

力

力是向量。

力是具有大小和方向的向量。

速度

速度是向量。

速度是具有大小和方向的向量。