分佈
- 什麼是正態分佈?
- 什麼是誤差幅度?
- 什麼是偏度?
- 什麼是峰度?
正態分佈
正態分佈曲線呈鐘形。
曲線的每個波段寬度為1個標準差
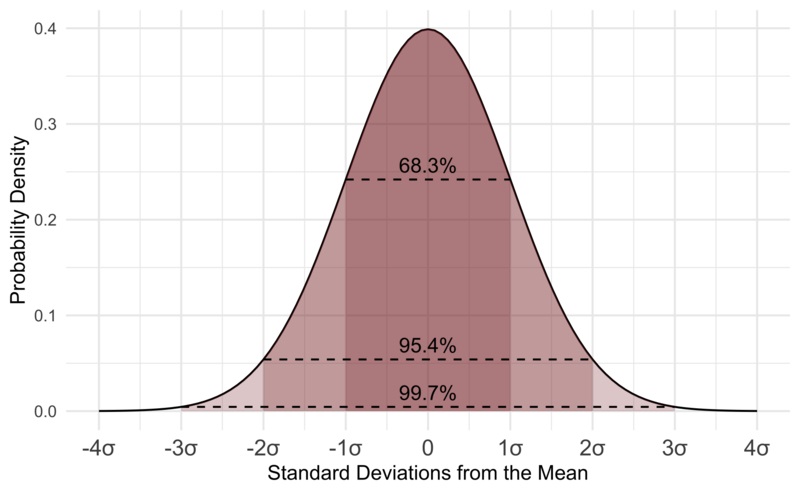
曲線的每個波段寬度為距平均值1個標準差。
距離1個標準差以內的值佔68.27%。
距離2個標準差以內的值佔95.45%。
距離3個標準差以內的值佔99.73%。
這意味著什麼?
大多數觀測值都在距平均值1個標準差以內。
幾乎所有觀測值都在2個標準差以內。
實際上所有觀測值都在3個標準差以內。
正態分佈事實
正態分佈是對稱的。峰值總是將分佈一分為二。
正態分佈是機率分佈。
許多觀測值遵循正態分佈
- 您的智商
- 您的體重
- 您的身高
- 您的薪水
- 您的血壓
正態分佈表明,接近平均值的值比遠離平均值的值更頻繁。
| 與平均值的距離 | 人口百分比 |
|---|---|
| 1個標準差 | 68.27% |
| 2個標準差 | 95.45% |
| 3個標準差 | 99.73% |
68-95-99.7 法則(又稱經驗法則)是一種記住正態分佈中不同波段內值百分比的速記法。
正態分佈也稱為高斯分佈和鐘形曲線。
誤差幅度
統計學家總是試圖以100%的準確性預測一切。
但是,總會有一些不確定性。
誤差幅度是量化這種統計不確定性的數字。
不同的幅度定義了我們認為可以找到正確答案的不同範圍。
可接受的幅度是一個判斷問題,並與答案的重要性有關。
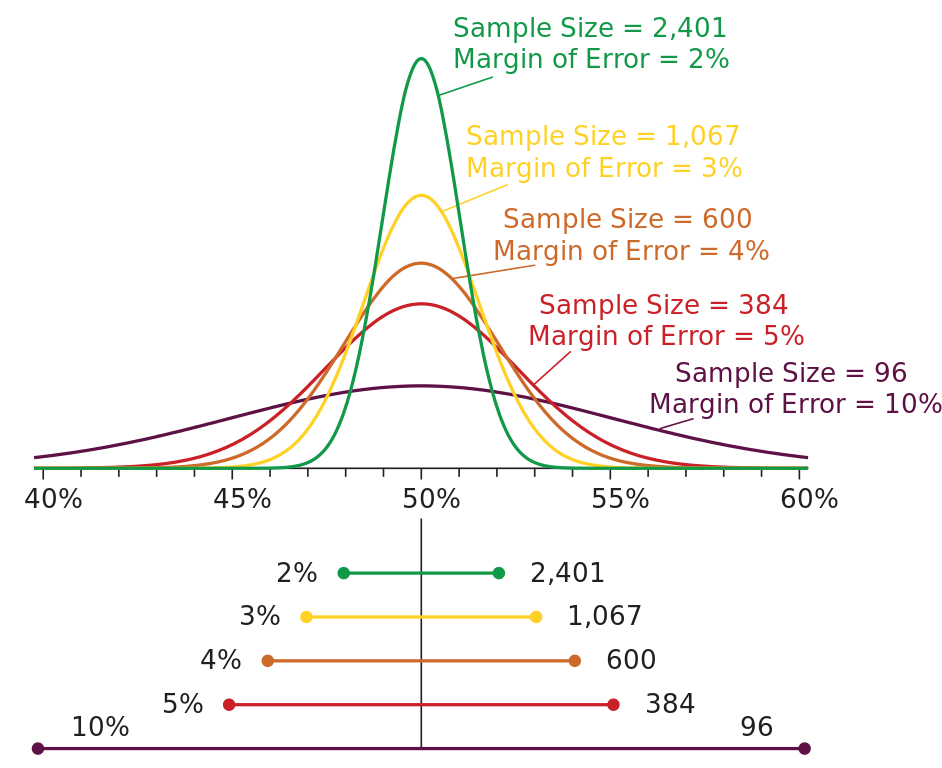
我們收集的樣本越多,誤差幅度越低。
如何解釋誤差幅度
假設有55%的抽樣人口表示他們計劃投“贊成”票。
當將其推算到整個人口時,您需要加/減誤差幅度,以給出可能的結果範圍。
誤差幅度為3%時,您可以確信有52%到58%的人會投“贊成”票。
誤差幅度為10%時,您可以確信有45%到65%的人會投“贊成”票。
偏度(Skewness)
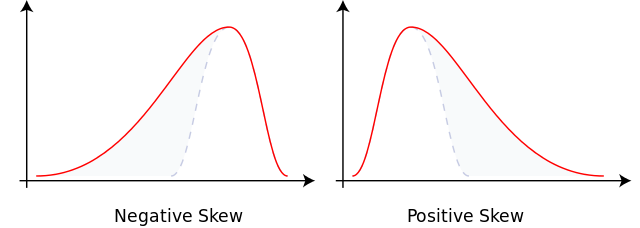
偏度是鐘形曲線(正態分佈)的一種扭曲(不對稱)。
峰度(Kurtosis)
峰度也是正態分佈(鐘形曲線)的一種扭曲。
偏度描述了一個尾部的意外值,而峰度描述了兩個尾部的意外值。
圖:負峰度(低於正態分佈)。
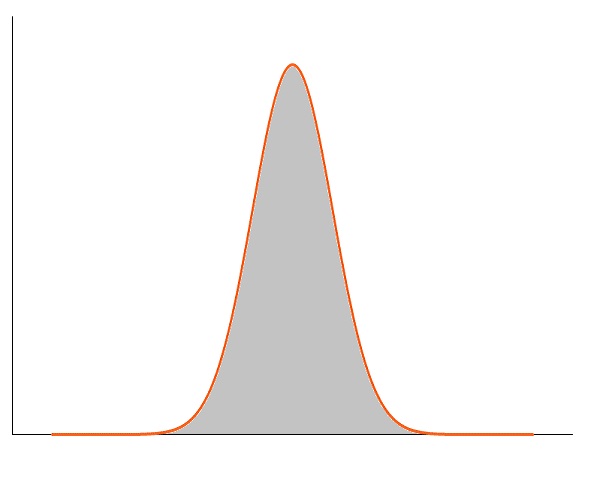
圖:正峰度(高於正態分佈)。