機器學習 - 線性迴歸
迴歸
當您嘗試找出變數之間的關係時,使用術語“迴歸”。
在機器學習和統計建模中,這種關係被用來預測未來事件的結果。
線性迴歸
線性迴歸利用資料點之間的關係來繪製一條穿過所有資料點的直線。
這條線可用於預測未來值。
在機器學習中,預測未來非常重要。
它是如何工作的?
Python 提供了查詢資料點之間關係並繪製線性迴歸線的方法。我們將向您展示如何使用這些方法,而不是透過數學公式。
在下面的示例中,x 軸代表年齡,y 軸代表速度。我們記錄了 13 輛汽車透過收費站時的年齡和速度。讓我們看看收集到的資料是否可以用於線性迴歸。
示例
首先繪製散點圖
import matplotlib.pyplot as plt
x = [5,7,8,7,2,17,2,9,4,11,12,9,6]
y = [99,86,87,88,111,86,103,87,94,78,77,85,86]
plt.scatter(x, y)
plt.show()
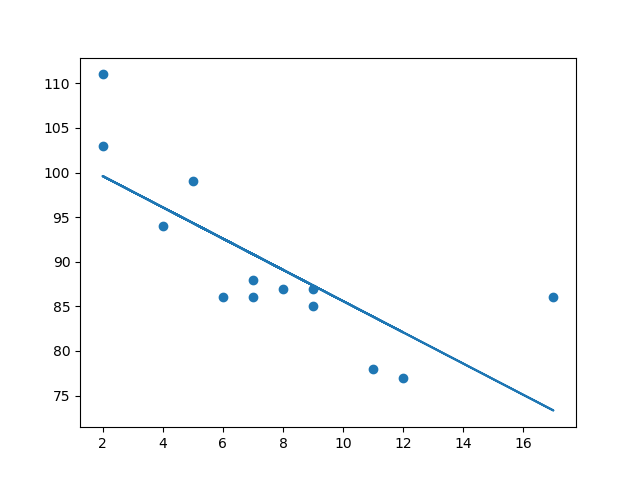
結果
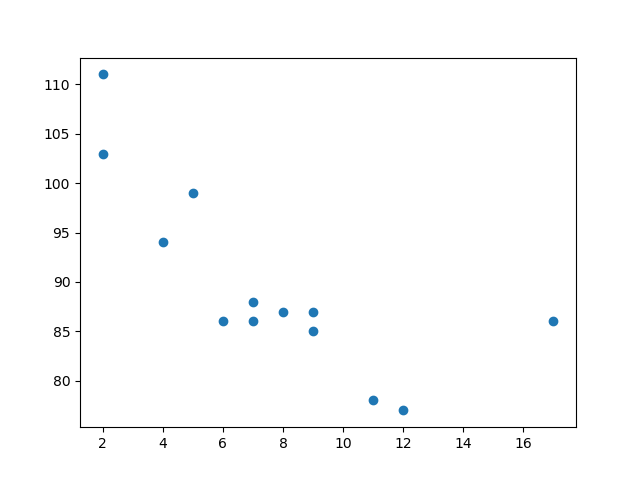
示例
匯入 scipy 並繪製線性迴歸線
import matplotlib.pyplot as plt
from scipy import stats
x = [5,7,8,7,2,17,2,9,4,11,12,9,6]
y = [99,86,87,88,111,86,103,87,94,78,77,85,86]
slope, intercept, r, p, std_err = stats.linregress(x, y)
def myfunc(x)
return slope * x + intercept
mymodel = list(map(myfunc, x))
plt.scatter(x, y)
plt.plot(x, mymodel)
plt.show()
結果

示例解釋
匯入所需的模組。
您可以在我們的 Matplotlib 教程 中瞭解 Matplotlib 模組。
您可以在我們的 SciPy 教程 中瞭解 SciPy 模組。
import matplotlib.pyplot as plt
from scipy import stats
建立代表 x 軸和 y 軸值的陣列
x = [5,7,8,7,2,17,2,9,4,11,12,9,6]
y = [99,86,87,88,111,86,103,87,94,78,77,85,86]
執行一個返回線性迴歸一些重要關鍵值的函式
slope, intercept, r, p, std_err = stats.linregress(x, y)
建立一個函式,該函式使用 slope 和 intercept 值來返回一個新值。這個新值表示對應 x 值的 y 軸位置
def myfunc(x)
return slope * x + intercept
將 x 陣列的每個值透過函式執行。這將生成一個包含新 y 軸值的新陣列
mymodel = list(map(myfunc, x))
繪製原始散點圖
plt.scatter(x, y)
繪製線性迴歸線
plt.plot(x, mymodel)
顯示圖表
plt.show()
R 代表相關性
瞭解 x 軸值和 y 軸值之間的關係很重要。如果沒有關係,線性迴歸就不能用於預測任何內容。
這種關係——相關係數——稱為 r。
r 值範圍從 -1 到 1,其中 0 表示無關係,1(和 -1)表示 100% 相關。
Python 和 Scipy 模組會為您計算此值,您只需將 x 和 y 值輸入即可。
示例
我的資料與線性迴歸的擬合程度如何?
from scipy import stats
x = [5,7,8,7,2,17,2,9,4,11,12,9,6]
y = [99,86,87,88,111,86,103,87,94,78,77,85,86]
slope, intercept, r, p, std_err = stats.linregress(x, y)
print(r)
自己動手試一試 »
注意:結果 -0.76 表明存在關係,雖然不完美,但表明我們可以將線性迴歸用於未來的預測。
預測未來值
現在我們可以利用收集到的資訊來預測未來值。
示例:讓我們嘗試預測一輛 10 年車齡汽車的速度。
為此,我們需要上面示例中的相同 myfunc() 函式
def myfunc(x)
return slope * x + intercept
示例
預測一輛 10 年車齡汽車的速度
from scipy import stats
x = [5,7,8,7,2,17,2,9,4,11,12,9,6]
y = [99,86,87,88,111,86,103,87,94,78,77,85,86]
slope, intercept, r, p, std_err = stats.linregress(x, y)
def myfunc(x)
return slope * x + intercept
speed = myfunc(10)
print(speed)
執行示例 »
示例預測速度為 85.6,我們也可以從圖表中讀出該值。
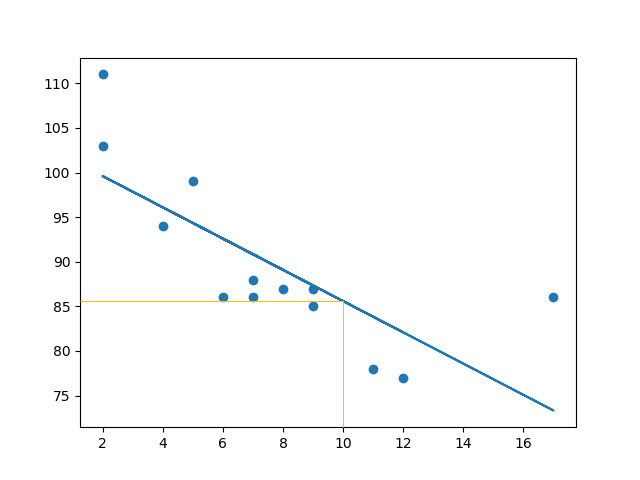
擬合效果差?
讓我們舉一個線性迴歸不是預測未來值的最佳方法的例子。
示例
這些 x 軸和 y 軸的值應該會導致線性迴歸的擬合效果非常差。
import matplotlib.pyplot as plt
from scipy import stats
x = [89,43,36,36,95,10,66,34,38,20,26,29,48,64,6,5,36,66,72,40]
y = [21,46,3,35,67,95,53,72,58,10,26,34,90,33,38,20,56,2,47,15]
slope, intercept, r, p, std_err = stats.linregress(x, y)
def myfunc(x)
return slope * x + intercept
mymodel = list(map(myfunc, x))
plt.scatter(x, y)
plt.plot(x, mymodel)
plt.show()
結果
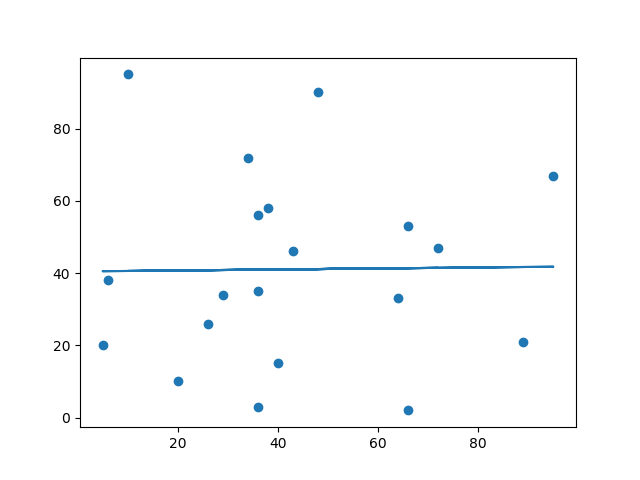
以及 r 的關係如何?
示例
您應該得到一個非常低的 r 值。
import numpy
from scipy import stats
x = [89,43,36,36,95,10,66,34,38,20,26,29,48,64,6,5,36,66,72,40]
y = [21,46,3,35,67,95,53,72,58,10,26,34,90,33,38,20,56,2,47,15]
slope, intercept, r, p, std_err = stats.linregress(x, y)
print(r)
自己動手試一試 »
結果:0.013 表明關係非常差,並告訴我們此資料集不適合進行線性迴歸。

