機器學習 - AUC - ROC 曲線
在此頁面上,W3schools.com 與 紐約資料科學學院 合作,為我們的學生提供數字培訓內容。
AUC - ROC 曲線
在分類中,有許多不同的評估指標。最流行的是準確率,它衡量模型正確的頻率。這是一個很好的指標,因為它易於理解,並且通常希望獲得最正確的猜測。在某些情況下,您可能需要考慮使用其他評估指標。
另一個常見的指標是 AUC,即接收者操作特徵 (ROC) 曲線下的面積。接收者操作特徵曲線繪製了不同分類閾值下的真陽性 (TP) 率與假陽性 (FP) 率。這些閾值是二元分類中分離兩個類別的不同機率截止點。它使用機率來告訴我們模型分離類別的效果。
不平衡資料
假設我們有一個不平衡資料集,其中大部分資料都是一個值。我們可以透過預測多數類別來獲得模型的高準確率。
示例
import numpy as np
來自 sklearn.metrics 匯入 accuracy_score, confusion_matrix, roc_auc_score, roc_curve
n = 10000
ratio = .95
n_0 = int((1-ratio) * n)
n_1 = int(ratio * n)
y = np.array([0] * n_0 + [1] * n_1)
# 以下是從一個總是預測多數類別的假設模型中獲得的機率
# 預測類別 1 的機率將是 100%
y_proba = np.array([1]*n)
y_pred = y_proba > .5
print(f'準確率分數: {accuracy_score(y, y_pred)}')
cf_mat = confusion_matrix(y, y_pred)
print('混淆矩陣')
print(cf_mat)
print(f'類別 0 準確率: {cf_mat[0][0]/n_0}')
print(f'類別 1 準確率: {cf_mat[1][1]/n_1}')
執行示例 »
廣告
儘管我們獲得了非常高的準確率,但該模型沒有提供任何關於資料的資訊,因此它沒有用處。我們 100% 準確地預測類別 1,同時 0% 不準確地預測類別 0。以準確率為代價,擁有一個能夠將兩個類別在某種程度上分開的模型可能會更好。
示例
# 以下是從一個不總是預測眾數的假設模型中獲得的機率
y_proba_2 = np.array(
np.random.uniform(0, .7, n_0).tolist() +
np.random.uniform(.3, 1, n_1).tolist()
)
y_pred_2 = y_proba_2 > .5
print(f'準確率分數: {accuracy_score(y, y_pred_2)}')
cf_mat = confusion_matrix(y, y_pred_2)
print('混淆矩陣')
print(cf_mat)
print(f'類別 0 準確率: {cf_mat[0][0]/n_0}')
print(f'類別 1 準確率: {cf_mat[1][1]/n_1}')
執行示例 »
對於第二組預測,我們的準確率分數不如第一組高,但每個類別的準確率更平衡。使用準確率作為評估指標,我們會將第一個模型評價為高於第二個模型,儘管它沒有告訴我們任何關於資料的資訊。
在這種情況下,更傾向於使用 AUC 等其他評估指標。
import matplotlib.pyplot as plt
def plot_roc_curve(true_y, y_prob)
"""
繪製基於機率的 roc 曲線
"""
fpr, tpr, thresholds = roc_curve(true_y, y_prob)
plt.plot(fpr, tpr)
plt.xlabel('假陽性率')
plt.ylabel('真陽性率')
示例
模型 1
plot_roc_curve(y, y_proba)
print(f'模型 1 AUC 分數: {roc_auc_score(y, y_proba)}')
結果
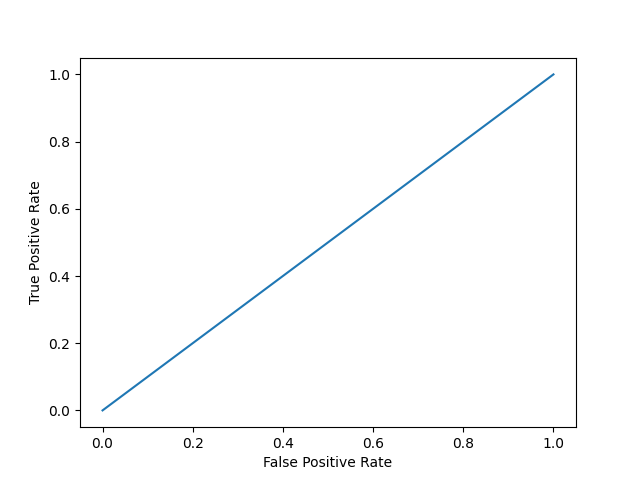
模型 1 AUC 分數: 0.5
示例
模型 2
plot_roc_curve(y, y_proba_2)
print(f'模型 2 AUC 分數: {roc_auc_score(y, y_proba_2)}')
結果
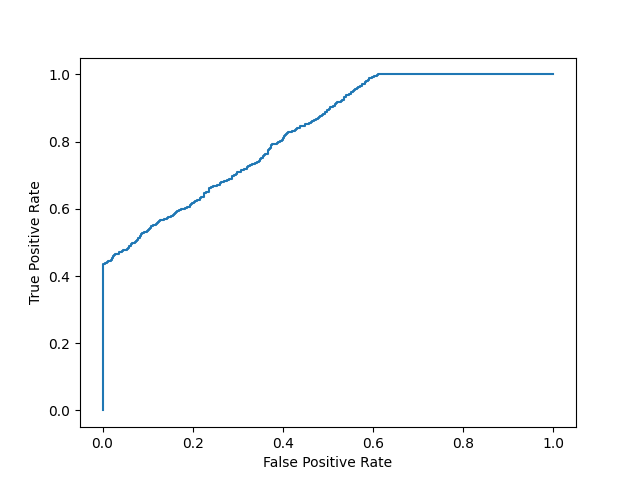
模型 2 AUC 分數: 0.8270551578947367
AUC 分數約為 0.5 表示模型無法區分兩個類別,曲線看起來像一條斜率為 1 的直線。AUC 分數越接近 1,表示模型有能力區分兩個類別,曲線將越接近圖表的左上角。
機率
由於 AUC 是一個利用類別預測機率的指標,因此即使兩個模型的準確率相似,我們也可以對 AUC 分數較高的模型比 AUC 分數較低的模型更有信心。
在下面的資料中,我們有兩組來自假設模型的機率。第一組的機率在預測兩個類別時不夠“自信”(機率接近 0.5)。第二組的機率在預測兩個類別時更“自信”(機率接近 0 或 1 的極端值)。
示例
import numpy as np
n = 10000
y = np.array([0] * n + [1] * n)
#
y_prob_1 = np.array(
np.random.uniform(.25, .5, n//2).tolist() +
np.random.uniform(.3, .7, n).tolist() +
np.random.uniform(.5, .75, n//2).tolist()
)
y_prob_2 = np.array(
np.random.uniform(0, .4, n//2).tolist() +
np.random.uniform(.3, .7, n).tolist() +
np.random.uniform(.6, 1, n//2).tolist()
)
print(f'模型 1 準確率分數: {accuracy_score(y, y_prob_1>.5)}')
print(f'模型 2 準確率分數: {accuracy_score(y, y_prob_2>.5)}')
print(f'模型 1 AUC 分數: {roc_auc_score(y, y_prob_1)}')
print(f'模型 2 AUC 分數: {roc_auc_score(y, y_prob_2)}')
執行示例 »
儘管兩個模型的準確率相似,但具有更高 AUC 分數的模型將更可靠,因為它考慮了預測機率。它在預測未來資料時更有可能為您提供更高的準確率。