機器學習 - 決策樹
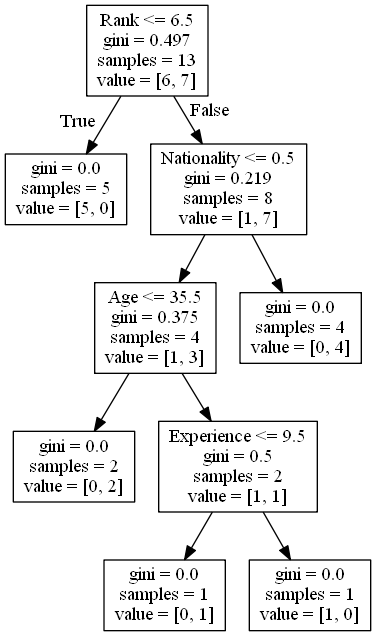
決策樹
在本章中,我們將向您展示如何製作一個“決策樹”。決策樹是一個流程圖,可以幫助您根據過去的經驗做出決策。
在示例中,一個人將嘗試決定他/她是否應該去看喜劇表演。
幸運的是,我們示例中的這個人記錄了每次有喜劇表演時的情況,並記錄了一些關於喜劇演員的資訊,還記錄了他們是否去看了。
| Age | 經驗 | 排名 | 國籍 | Go |
| 36 | 10 | 9 | UK | 不推薦 |
| 42 | 12 | 4 | USA | 不推薦 |
| 23 | 4 | 6 | N | 不推薦 |
| 52 | 4 | 4 | USA | 不推薦 |
| 43 | 21 | 8 | USA | 推薦 |
| 44 | 14 | 5 | UK | 不推薦 |
| 66 | 3 | 7 | N | 推薦 |
| 35 | 14 | 9 | UK | 推薦 |
| 52 | 13 | 7 | N | 推薦 |
| 35 | 5 | 9 | N | 推薦 |
| 24 | 3 | 5 | USA | 不推薦 |
| 18 | 3 | 7 | UK | 推薦 |
| 45 | 9 | 9 | UK | 推薦 |
現在,基於這個資料集,Python 可以建立一個決策樹,用於決定是否有新的表演值得參加。
它是如何工作的?
首先,使用 pandas 讀取資料集
要製作決策樹,所有資料都必須是數值的。
我們需要將非數值列 'Nationality' 和 'Go' 轉換為數值。
Pandas 有一個 map() 方法,它接受一個字典,其中包含有關如何轉換值的資訊。
{'UK': 0, 'USA': 1, 'N': 2}
表示將值 'UK' 轉換為 0,'USA' 轉換為 1,'N' 轉換為 2。
示例
將字串值更改為數值
d = {'UK': 0, 'USA': 1, 'N': 2}
df['Nationality'] = df['Nationality'].map(d)
d = {'YES': 1, 'NO': 0}
df['Go'] = df['Go'].map(d)
print(df)
然後,我們必須將特徵列與目標列分開。
特徵列是我們嘗試從中預測的列,目標列是我們嘗試預測其值的列。
示例
X 是特徵列,y 是目標列
features = ['Age', 'Experience', 'Rank', 'Nationality']
X = df[features]
y = df['Go']
print(X)
print(y)
現在我們可以建立實際的決策樹,並用我們的詳細資訊對其進行擬合。首先匯入我們需要的模組
示例
建立並顯示決策樹
import pandas
from sklearn import tree
來自 sklearn.tree 匯入 DecisionTreeClassifier
import matplotlib.pyplot as plt
df = pandas.read_csv("data.csv")
d = {'UK': 0, 'USA': 1, 'N': 2}
df['Nationality'] = df['Nationality'].map(d)
d = {'YES': 1, 'NO': 0}
df['Go'] = df['Go'].map(d)
features = ['Age', 'Experience', 'Rank', 'Nationality']
X = df[features]
y = df['Go']
dtree = DecisionTreeClassifier()
dtree = dtree.fit(X, y)
tree.plot_tree(dtree, feature_names=features)
結果解釋
決策樹使用您先前的決策來計算您想去看喜劇演員表演的可能性。
讓我們來解讀決策樹的各個方面

排名
Rank <= 6.5 意味著所有排名為 6.5 或更低的喜劇演員將沿著 True 箭頭(左側)前進,其餘的將沿著 False 箭頭(右側)前進。
gini = 0.497 指的是劃分的質量,並且始終是一個介於 0.0 和 0.5 之間的數字,其中 0.0 意味著所有樣本都得到了相同的結果,而 0.5 意味著劃分恰好在中間。
samples = 13 意味著在決策的這一點上還有 13 位喜劇演員,因為這是第一步,所以就是所有演員。
value = [6, 7] 意味著在這 13 位喜劇演員中,6 位會得到“否”,7 位會得到“是”。
基尼指數
劃分樣本有很多方法,在本教程中我們使用基尼指數法。
基尼指數法使用此公式
Gini = 1 - (x/n)2 - (y/n)2
其中 x 是正面答案(“是”)的數量,n 是樣本總數,y 是負面答案(“否”)的數量,這使我們得到以下計算
1 - (7 / 13)2 - (6 / 13)2 = 0.497
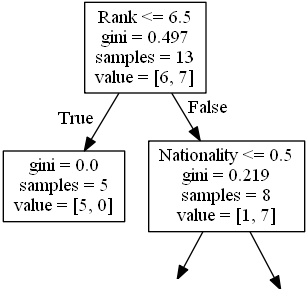
下一步包含兩個框,一個框用於排名為 6.5 或更低的喜劇演員,另一個框用於其餘的。
True - 5 位喜劇演員在此結束
gini = 0.0 意味著所有樣本都得到了相同的結果。
samples = 5 意味著在此分支中還有 5 位喜劇演員(排名為 6.5 或更低的 5 位喜劇演員)。
value = [5, 0] 意味著 5 位得到“否”,0 位得到“是”。
False - 8 位喜劇演員繼續
國籍
Nationality <= 0.5 意味著國籍值為 0.5 或更低的喜劇演員將沿著左側箭頭前進(這意味著所有來自英國的喜劇演員),其餘的將沿著右側箭頭前進。
gini = 0.219 意味著大約 22% 的樣本會走向一個方向。
samples = 8 意味著在此分支中還有 8 位喜劇演員(排名高於 6.5 的 8 位喜劇演員)。
value = [1, 7] 意味著在這 8 位喜劇演員中,1 位會得到“否”,7 位會得到“是”。
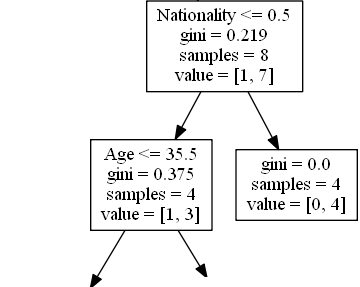
True - 4 位喜劇演員繼續
Age
Age <= 35.5 意味著年齡在 35.5 歲或以下的喜劇演員將沿著左側箭頭前進,其餘的將沿著右側箭頭前進。
gini = 0.375 意味著大約 37.5% 的樣本會走向一個方向。
samples = 4 意味著在此分支中還有 4 位喜劇演員(4 位來自英國的喜劇演員)。
value = [1, 3] 意味著在這 4 位喜劇演員中,1 位會得到“否”,3 位會得到“是”。
False - 4 位喜劇演員在此結束
gini = 0.0 意味著所有樣本都得到了相同的結果。
samples = 4 意味著在此分支中還有 4 位喜劇演員(4 位不是來自英國的喜劇演員)。
value = [0, 4] 意味著在這 4 位喜劇演員中,0 位會得到“否”,4 位會得到“是”。
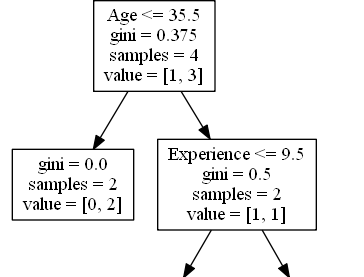
True - 2 位喜劇演員在此結束
gini = 0.0 意味著所有樣本都得到了相同的結果。
samples = 2 意味著在此分支中還有 2 位喜劇演員(年齡在 35.5 歲或以下的 2 位喜劇演員)。
value = [0, 2] 意味著在這 2 位喜劇演員中,0 位會得到“否”,2 位會得到“是”。
False - 2 位喜劇演員繼續
經驗
Experience <= 9.5 意味著擁有 9.5 年或更少經驗的喜劇演員將沿著左側箭頭前進,其餘的將沿著右側箭頭前進。
gini = 0.5 意味著 50% 的樣本會走向一個方向。
samples = 2 意味著在此分支中還有 2 位喜劇演員(年齡大於 35.5 歲的 2 位喜劇演員)。
value = [1, 1] 意味著在這 2 位喜劇演員中,1 位會得到“否”,1 位會得到“是”。
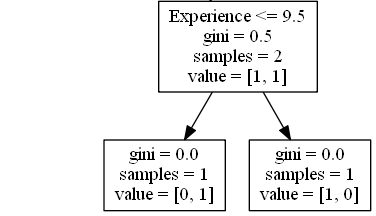
True - 1 位喜劇演員在此結束
gini = 0.0 意味著所有樣本都得到了相同的結果。
samples = 1 意味著在此分支中還有 1 位喜劇演員(擁有 9.5 年或更少經驗的 1 位喜劇演員)。
value = [0, 1] 意味著 0 位會得到“否”,1 位會得到“是”。
False - 1 位喜劇演員在此結束
gini = 0.0 意味著所有樣本都得到了相同的結果。
samples = 1 意味著在此分支中還有 1 位喜劇演員(擁有超過 9.5 年經驗的 1 位喜劇演員)。
value = [1, 0] 意味著 1 位會得到“否”,0 位會得到“是”。
預測值
我們可以使用決策樹來預測新值。
例如:我應該去看一位 40 歲、美國籍、有 10 年經驗、喜劇排名為 7 的喜劇演員的表演嗎?
不同結果
您會發現,如果您多次執行決策樹,即使輸入相同的資料,它也會給出不同的結果。
這是因為決策樹不能給出 100% 確定的答案。它是基於結果的機率,答案會有所不同。

