機器學習 - 混淆矩陣
在此頁面上,W3schools.com 與 紐約資料科學學院 合作,為我們的學生提供數字培訓內容。
什麼是混淆矩陣?
它是一個在分類問題中用於評估模型錯誤所在的表格。
行代表實際應該為的類別。列代表我們做出的預測。使用此表格可以輕鬆檢視哪些預測是錯誤的。
建立混淆矩陣
可以透過邏輯迴歸進行的預測來建立混淆矩陣。
現在,我們將使用 NumPy 來生成實際值和預測值。
import numpy
接下來,我們需要生成“實際”和“預測”值的數字。
actual = numpy.random.binomial(1, 0.9, size = 1000)
predicted = numpy.random.binomial(1, 0.9, size = 1000)
為了建立混淆矩陣,我們需要從 sklearn 模組匯入 metrics。
from sklearn import metrics
匯入 metrics 後,我們就可以在實際值和預測值上使用混淆矩陣函式。
confusion_matrix = metrics.confusion_matrix(actual, predicted)
為了建立更易於理解的視覺化顯示,我們需要將表格轉換為混淆矩陣顯示。
cm_display = metrics.ConfusionMatrixDisplay(confusion_matrix = confusion_matrix, display_labels = [0, 1])
視覺化顯示需要我們從 matplotlib 匯入 pyplot。
import matplotlib.pyplot as plt
最後,我們可以使用 pyplot 的 plot() 和 show() 函式來顯示圖表。
cm_display.plot()
plt.show()
觀看整個示例的實際演示
示例
import matplotlib.pyplot as plt
import numpy
from sklearn import metrics
actual = numpy.random.binomial(1,.9,size = 1000)
predicted = numpy.random.binomial(1,.9,size = 1000)
confusion_matrix = metrics.confusion_matrix(actual, predicted)
cm_display = metrics.ConfusionMatrixDisplay(confusion_matrix = confusion_matrix, display_labels = [0, 1])
cm_display.plot()
plt.show()
結果
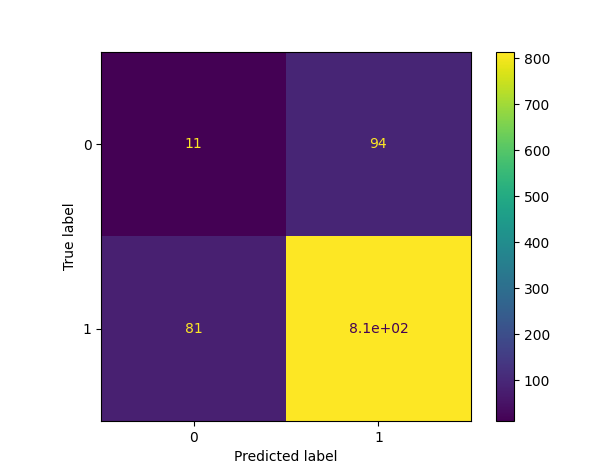
結果解釋
建立的混淆矩陣有四個不同的象限
真負例(左上角象限)
假正例(右上角象限)
假負例(左下角象限)
真正例(右下角象限)
真表示預測值準確,假表示有錯誤或預測錯誤。
現在我們已經建立了一個混淆矩陣,我們可以計算不同的指標來量化模型的質量。首先,我們來看一下準確率。
廣告
建立的指標
該矩陣為我們提供了許多有用的指標,可以幫助我們評估分類模型。
不同的度量包括:準確率、精確率、召回率(靈敏度)、特異度和 F1 分數,如下所述。
準確率
準確率衡量模型在多大程度上是正確的。
如何計算
(真正例 + 真負例) / 總預測數
精確率
在預測為正例的樣本中,有多少比例是真正的正例?
如何計算
真正例 / (真正例 + 假正例)
精確率不評估正確預測的負例。
召回率(靈敏度)
在所有實際為正例的樣本中,有多少比例被預測為正例?
召回率(有時也稱為靈敏度)衡量模型預測正例的準確性。
這意味著它關注真正例和假負例(即被錯誤預測為負例的正例)。
如何計算
真正例 / (真正例 + 假負例)
召回率有助於理解模型預測某個例項為正例的程度。
特異度
模型預測負例的準確性如何?
特異度與召回率相似,但從負例的角度來看。
如何計算
真負例 / (真負例 + 假正例)
由於它與召回率正好相反,我們使用 recall_score 函式,傳入相反的標籤(pos_label=0)。
F1 分數
F1 分數是精確率和召回率的“調和平均數”。
它同時考慮了假正例和假負例,並且對於不平衡資料集很有用。
如何計算
2 * ((精確率 * 召回率) / (精確率 + 召回率))
此分數不考慮真負例。
所有計算合在一起
示例
#metrics
print({"Accuracy":Accuracy,"Precision":Precision,"Sensitivity_recall":Sensitivity_recall,"Specificity":Specificity,"F1_score":F1_score})
執行示例 »

