機器學習 - K 近鄰 (KNN)
在此頁面上,W3schools.com 與 紐約資料科學學院 合作,為我們的學生提供數字培訓內容。
KNN
KNN 是一種簡單、監督式的機器學習 (ML) 演算法,可用於分類或迴歸任務,並且經常用於缺失值填充。它的基本思想是,給定資料點最近的觀測值是資料集中最“相似”的觀測值,因此我們可以根據最接近的現有資料點的值來對未知的點進行分類。透過選擇 K,使用者可以選擇要在演算法中使用多少個附近的觀測值。
在這裡,我們將向您展示如何實現 KNN 演算法進行分類,並展示不同 K 值如何影響結果。
它是如何工作的?
K 是要使用的最近鄰的數量。對於分類,多數投票用於確定新觀測值應屬於哪個類別。較大的 K 值通常對異常值更具魯棒性,並且比非常小的值產生更穩定的決策邊界(K=3 比 K=1 更好,後者可能會產生不良結果。
示例
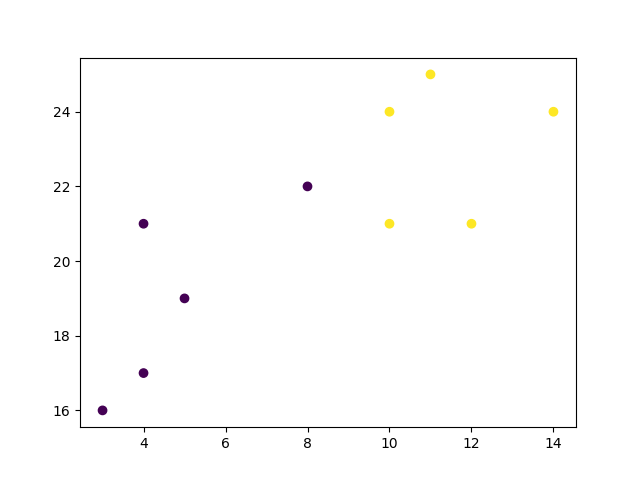
首先,視覺化一些資料點
import matplotlib.pyplot as plt
x = [4, 5, 10, 4, 3, 11, 14 , 8, 10, 12]
y = [21, 19, 24, 17, 16, 25, 24, 22, 21, 21]
classes = [0, 0, 1, 0, 0, 1, 1, 0, 1, 1]
plt.scatter(x, y, c=classes)
plt.show()
結果
廣告
現在,我們使用 K=1 來擬合 KNN 演算法
from sklearn.neighbors import KNeighborsClassifier
data = list(zip(x, y))
knn = KNeighborsClassifier(n_neighbors=1)
knn.fit(data, classes)
並使用它來分類新的資料點
示例
new_x = 8
new_y = 21
new_point = [(new_x, new_y)]
prediction = knn.predict(new_point)
plt.scatter(x + [new_x], y + [new_y], c=classes + [prediction[0]])
plt.text(x=new_x-1.7, y=new_y-0.7, s=f"new point, class: {prediction[0]}")
plt.show()
結果
現在,我們做同樣的事情,但使用一個更高的 K 值,這會改變預測結果
示例
knn = KNeighborsClassifier(n_neighbors=5)
knn.fit(data, classes)
prediction = knn.predict(new_point)
plt.scatter(x + [new_x], y + [new_y], c=classes + [prediction[0]])
plt.text(x=new_x-1.7, y=new_y-0.7, s=f"new point, class: {prediction[0]}")
plt.show()
結果
示例解釋
匯入所需的模組。
你可以在我們的 “Matplotlib 教程”中瞭解 Matplotlib 模組。
scikit-learn 是 Python 中一個流行的機器學習庫。
import matplotlib.pyplot as plt
from sklearn.neighbors import KNeighborsClassifier
建立類似資料集變數的陣列。我們有兩個輸入特徵(`x` 和 `y`),然後是一個目標類別(`class`)。帶有目標類別的輸入特徵將用於預測新資料的類別。請注意,雖然我們這裡只使用了兩個輸入特徵,但此方法適用於任何數量的變數
x = [4, 5, 10, 4, 3, 11, 14 , 8, 10, 12]
y = [21, 19, 24, 17, 16, 25, 24, 22, 21, 21]
classes = [0, 0, 1, 0, 0, 1, 1, 0, 1, 1]
將輸入特徵轉換為一組點
data = list(zip(x, y))
print(data)
結果
[(4, 21), (5, 19), (10, 24), (4, 17), (3, 16), (11, 25), (14, 24), (8, 22), (10, 21), (12, 21)]
使用輸入特徵和目標類別,我們在模型上使用 1 個最近鄰擬合 KNN 模型
knn = KNeighborsClassifier(n_neighbors=1)
knn.fit(data, classes)
然後,我們可以使用同一個 KNN 物件來預測新的、未預測資料點的類別。首先,我們建立新的 x 和 y 特徵,然後呼叫 knn.predict() 來獲取 0 或 1 的類別
new_x = 8
new_y = 21
new_point = [(new_x, new_y)]
prediction = knn.predict(new_point)
print(prediction)
結果
[0]
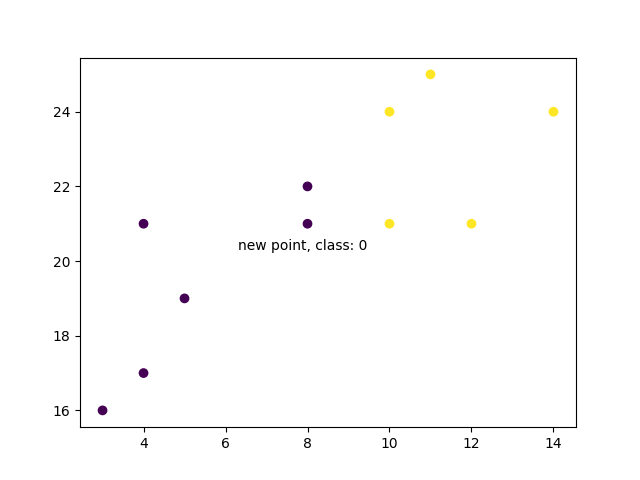
當我們繪製所有資料以及新點和類別時,我們可以看到它已被標記為藍色,屬於 1 類別。文字註釋只是為了突出顯示新點的位置
plt.scatter(x + [new_x], y + [new_y], c=classes + [prediction[0]])
plt.text(x=new_x-1.7, y=new_y-0.7, s=f"new point, class: {prediction[0]}")
plt.show()
結果

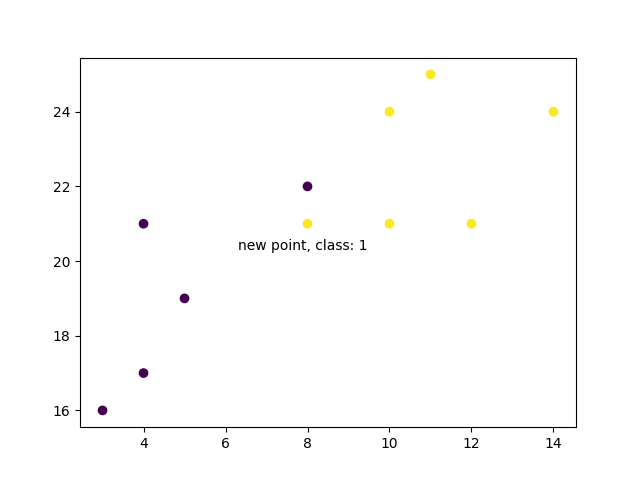
但是,當我們改變鄰居的數量為 5 時,用於對新點進行分類的點數會改變。結果,新點的分類也隨之改變
knn = KNeighborsClassifier(n_neighbors=5)
knn.fit(data, classes)
prediction = knn.predict(new_point)
print(prediction)
結果
[1]
當我們繪製新點的類別以及舊點時,我們會注意到顏色已根據關聯的類別標籤發生變化
plt.scatter(x + [new_x], y + [new_y], c=classes + [prediction[0]])
plt.text(x=new_x-1.7, y=new_y-0.7, s=f"new point, class: {prediction[0]}")
plt.show()
結果


