資料科學 - 迴歸表:R 方
R 方
R 方和調整 R 方描述了線性迴歸模型對資料點的擬合程度
R 方的值總是在 0 到 1 之間(0% 到 100%)。
- 高 R 方值表示許多資料點接近線性迴歸函式線。
- 低 R 方值表示線性迴歸函式線與資料擬合不佳。
低 R 方值(0.00)的視覺示例
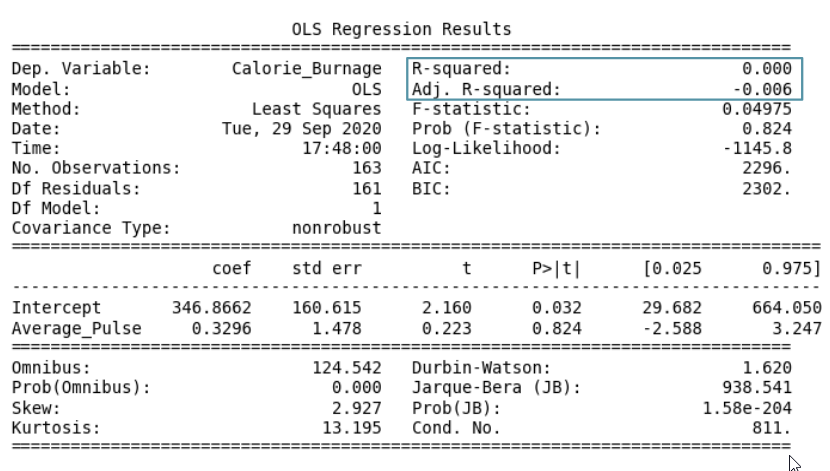
我們的迴歸模型顯示 R 方值為零,這意味著線性迴歸函式線與資料擬合不佳。
當我們繪製 Average_Pulse 和 Calorie_Burnage 的散點圖以及線性迴歸函式時,可以看到這一點。
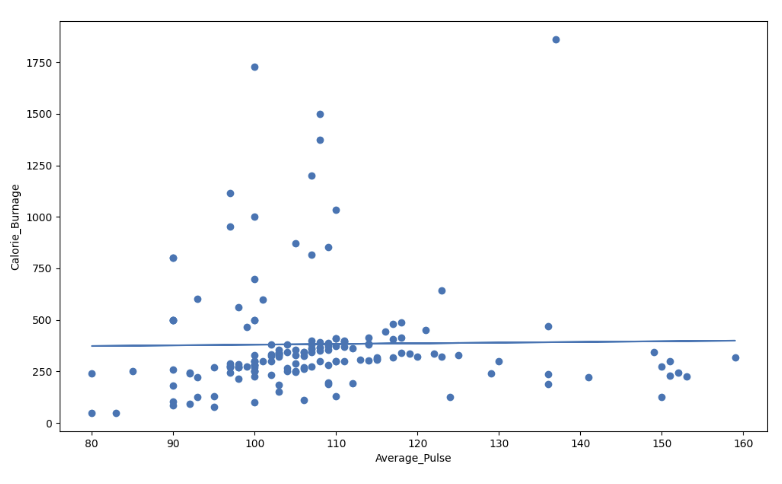
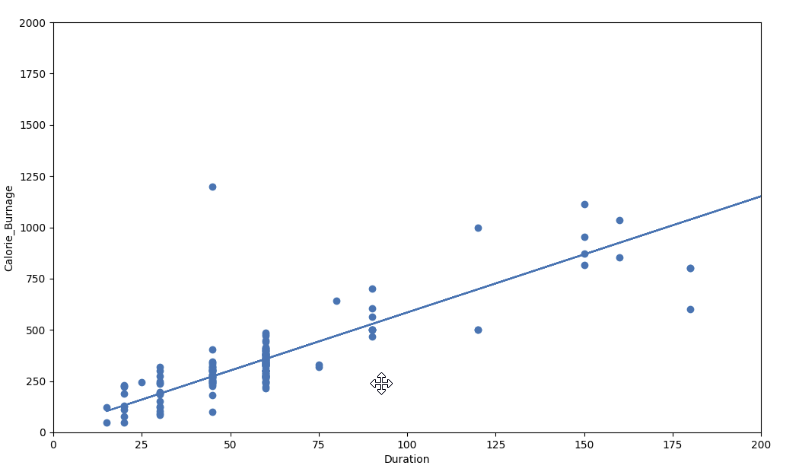
高 R 方值(0.79)的視覺示例
但是,如果我們繪製 **Duration** 和 **Calorie_Burnage**,R 方會增加。這裡,我們看到資料點接近線性迴歸函式線。
這是 Python 程式碼
示例
import pandas as pd
import matplotlib.pyplot as plt
from scipy import stats
full_health_data = pd.read_csv("data.csv", header=0, sep=",")
x = full_health_data["Duration"]
y = full_health_data ["Calorie_Burnage"]
slope, intercept, r, p, std_err = stats.linregress(x, y)
def myfunc(x)
return slope * x + intercept
mymodel = list(map(myfunc, x))
print(mymodel)
plt.scatter(x, y)
plt.plot(x, mymodel)
plt.ylim(ymin=0, ymax=2000)
plt.xlim(xmin=0, xmax=200)
plt.xlabel("Duration")
plt.ylabel ("Calorie_Burnage")
plt.show()
自己動手試一試 »
總結 - 使用 Average_Pulse 預測 Calorie_Burnage
如何總結以 Average_Pulse 為解釋變數的線性迴歸函式?
- 係數為 0.3296,這意味著 Average_Pulse 對 Calorie_Burnage 的影響非常小。
- 高 P 值(0.824)表示我們無法得出 Average_Pulse 和 Calorie_Burnage 之間存在關係的結論。
- R 方值為 0,這意味著線性迴歸函式線與資料擬合不佳。

