資料科學 - 線性迴歸
我們遺漏了一個影響 Calorie_Burnage 的重要變數,那就是訓練課程的 Duration(時長)。
Duration(時長)與 Average_Pulse(平均脈搏)結合起來,將能更精確地解釋 Calorie_Burnage(消耗的卡路里)。
線性迴歸
當你試圖找出變數之間的關係時,就會用到 regression(迴歸)這個術語。
在機器學習和統計建模中,這種關係被用來預測事件的結果。
在本模組中,我們將介紹以下問題:
- 我們能否得出結論:Average_Pulse(平均脈搏)和 Duration(時長)與 Calorie_Burnage(消耗的卡路里)相關?
- 我們能否利用 Average_Pulse(平均脈搏)和 Duration(時長)來預測 Calorie_Burnage(消耗的卡路里)?
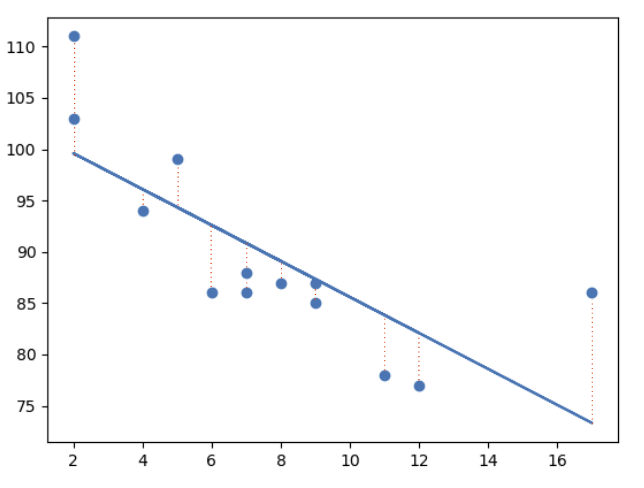
最小二乘法
線性迴歸使用最小二乘法。
其概念是繪製一條穿過所有散點圖資料點的直線。這條直線的位置是為了最小化所有資料點到直線的距離。
這個距離被稱為“殘差”或“誤差”。
紅色的虛線表示資料點到繪製的數學函式的距離。
單解釋變數線性迴歸
在此示例中,我們將嘗試使用線性迴歸來透過 Average_Pulse(平均脈搏)預測 Calorie_Burnage(消耗的卡路里)。
示例
import pandas as pd
import matplotlib.pyplot as plt
from scipy import stats
full_health_data = pd.read_csv("data.csv", header=0, sep=",")
x = full_health_data["Average_Pulse"]
y = full_health_data ["Calorie_Burnage"]
slope, intercept, r, p, std_err = stats.linregress(x, y)
def myfunc(x)
return slope * x + intercept
mymodel = list(map(myfunc, x))
plt.scatter(x, y)
plt.plot(x, slope * x + intercept)
plt.ylim(ymin=0, ymax=2000)
plt.xlim(xmin=0, xmax=200)
plt.xlabel("Average_Pulse")
plt.ylabel ("Calorie_Burnage")
plt.show()
自己動手試一試 »
示例解釋
- 匯入所需的模組:Pandas、matplotlib 和 Scipy
- 將 Average_Pulse(平均脈搏)隔離為 x。將 Calorie_burnage(消耗的卡路里)隔離為 y。
- 使用:slope, intercept, r, p, std_err = stats.linregress(x, y) 獲取重要的關鍵值。
- 建立一個函式,該函式使用斜率 (slope) 和截距 (intercept) 值來返回一個新值。這個新值代表了對應 x 值在 y 軸上的位置。
- 將 x 陣列的每個值透過函式執行。這將產生一個包含新的 y 軸值的陣列:mymodel = list(map(myfunc, x))
- 繪製原始散點圖:plt.scatter(x, y)
- 繪製線性迴歸線:plt.plot(x, mymodel)
- 定義座標軸的最大值和最小值。
- 標註座標軸:“Average_Pulse”(平均脈搏)和“Calorie_Burnage”(消耗的卡路里)。
輸出
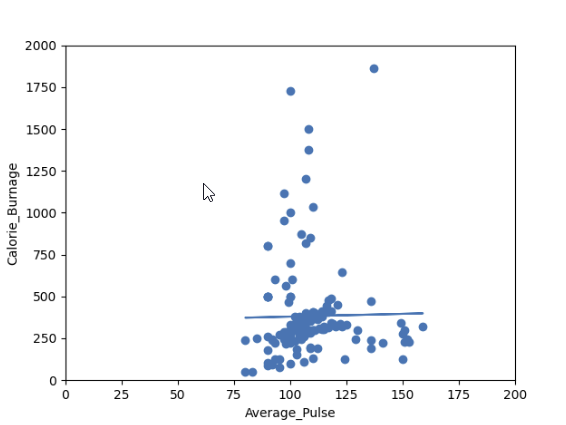
您認為這條線能夠精確地預測 Calorie_Burnage(消耗的卡路里)嗎?
我們將證明,僅憑 Average_Pulse(平均脈搏)變數不足以精確預測 Calorie_Burnage(消耗的卡路里)。

