資料科學 - 線性迴歸案例
案例:使用 Duration + Average_Pulse 預測 Calorie_Burnage
建立使用 Average_Pulse 和 Duration 作為解釋變數的線性迴歸表
示例
import pandas as pd
import statsmodels.formula.api as smf
full_health_data = pd.read_csv("data.csv", header=0, sep=",")
model = smf.ols('Calorie_Burnage ~ Average_Pulse + Duration', data = full_health_data)
results = model.fit()
print(results.summary())
自己動手試一試 »
示例解釋
- 匯入庫 statsmodels.formula.api as smf。Statsmodels 是 Python 中的一個統計庫。
- 使用 full_health_data 資料集。
- 使用 smf.ols() 基於普通最小二乘法建立模型。請注意,解釋變數必須寫在括號中的第一個位置。使用 full_health_data 資料集。
- 透過呼叫 .fit(),您將獲得 results 變數。它包含有關回歸模型的許多資訊。
- 呼叫 summary() 以獲取線性迴歸結果的表格。
輸出
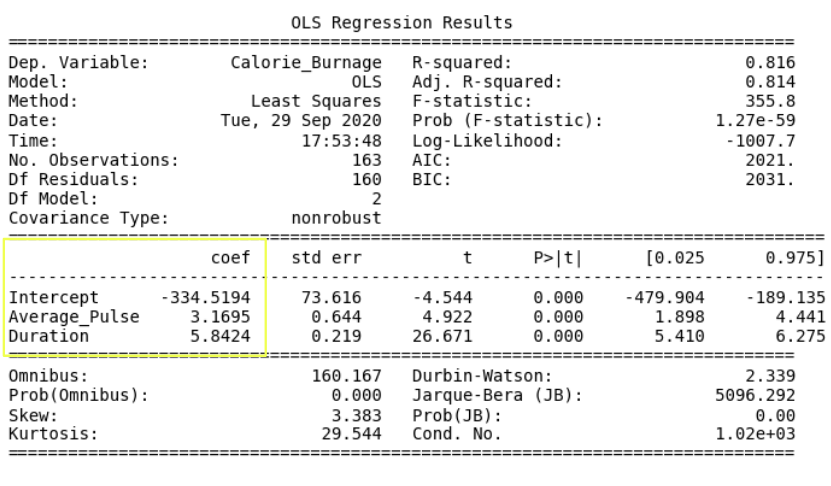
線性迴歸函式可以用數學方式重寫為:
Calorie_Burnage = Average_Pulse * 3.1695 + Duration * 5.8424 - 334.5194
四捨五入到兩位小數
Calorie_Burnage = Average_Pulse * 3.17 + Duration * 5.84 - 334.52
在 Python 中定義線性迴歸函式
在 Python 中定義線性迴歸函式以執行預測。
如果
- Average pulse 為 110,訓練課程時長為 60 分鐘,Calorie_Burnage 是多少?
- Average pulse 為 140,訓練課程時長為 45 分鐘,Calorie_Burnage 是多少?
- Average pulse 為 175,訓練課程時長為 20 分鐘,Calorie_Burnage 是多少?
示例
def Predict_Calorie_Burnage(Average_Pulse, Duration)
return(3.1695*Average_Pulse + 5.8434 * Duration - 334.5194)
print(Predict_Calorie_Burnage(110,60))
print(Predict_Calorie_Burnage(140,45))
print(Predict_Calorie_Burnage(175,20))
自己動手試一試 »
答案
- Average pulse 為 110,訓練課程時長為 60 分鐘 = 365 卡路里
- Average pulse 為 140,訓練課程時長為 45 分鐘 = 372 卡路里
- Average pulse 為 175,訓練課程時長為 20 分鐘 = 337 卡路里
訪問係數
檢視係數
- 如果 Average_Pulse 增加一,Calorie_Burnage 增加 3.17。
- 如果 Duration 增加一,Calorie_Burnage 增加 5.84。
訪問 P 值
檢視每個係數的 P 值。
- Average_Pulse、Duration 和 Intercept 的 P 值為 0.00。
- 由於 P 值小於 0.05,因此所有變數的 P 值在統計上都顯著。
因此,我們可以得出結論,Average_Pulse 和 Duration 與 Calorie_Burnage 之間存在關係。
調整 R 平方
如果我們有多個解釋變數,R 平方會存在問題。
如果我們新增更多變數,R 平方几乎總會增加,並且永遠不會減少。
這是因為我們線上性迴歸函數週圍添加了更多資料點。
如果我們新增與 Calorie_Burnage 無關的隨機變數,我們就有可能錯誤地認為線性迴歸函式是一個好的擬合。調整 R 平方可以解決這個問題。
因此,如果我們有多個解釋變數,最好檢視調整後的 R 平方值。
調整後的 R 平方值為 0.814。
R 平方值始終在 0 到 1 之間(0% 到 100%)。
- 較高的 R 平方值表示許多資料點接近線性迴歸函式線。
- 較低的 R 平方值表示線性迴歸函式線與資料的擬合度不佳。
結論:模型很好地擬合了資料點!
恭喜!您已完成資料科學庫的最後一章。

