二項式分佈
二項式分佈
二項式分佈是離散分佈。
它描述了二元場景的結果,例如拋硬幣,結果只可能是正面或反面。
它有三個引數
n - 試驗次數。
p - 每次試驗發生的機率(例如,拋硬幣時每次試驗的機率為 0.5)。
size - 返回陣列的形狀。
離散分佈:分佈定義在一組獨立的事件上,例如,拋硬幣的結果是離散的,因為它只能是正面或反面,而人的身高是連續的,它可以是 170、170.1、170.11 等。
示例
給定 10 次拋硬幣試驗,生成 10 個數據點
from numpy import random
x = random.binomial(n=10, p=0.5, size=10)
print(x)
自己動手試一試 »
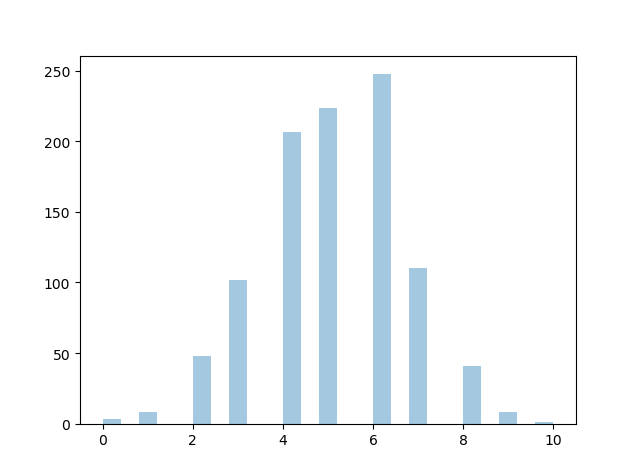
二項式分佈視覺化
示例
from numpy import random
import matplotlib.pyplot as plt
import seaborn as sns
sns.distplot(random.binomial(n=10, p=0.5, size=1000), hist=True, kde=False)
plt.show()
結果
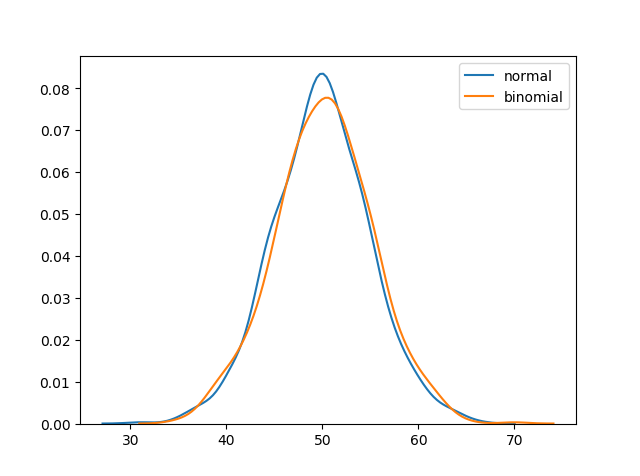
正態分佈與二項式分佈的區別
主要區別在於正態分佈是連續的,而二項式分佈是離散的,但如果有足夠多的資料點,它將與具有特定位置和尺度的正態分佈非常相似。
示例
from numpy import random
import matplotlib.pyplot as plt
import seaborn as sns
sns.distplot(random.normal(loc=50, scale=5, size=1000), hist=False, label='normal')
sns.distplot(random.binomial(n=100, p=0.5, size=1000), hist=False, label='binomial')
plt.show()
結果